题目
6.证明:点列(Pn(xn,yn)收敛于P0 (x0,y0)的充要条件是 lim {x)_(n)=(x)_(0) 和 lim (y)_(n)=(y)_(0).
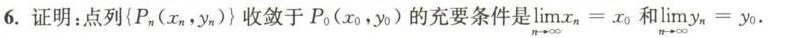
题目解答
答案
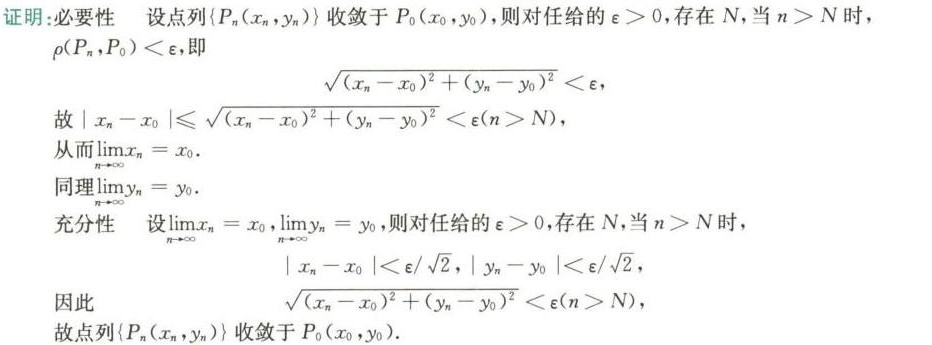
解析
步骤 1:必要性证明
假设点列{Pn(xn,yn)}收敛于P0(x0,y0),则对任意给定的正数ε,存在正整数N,当n>N时,有
$$
\rho(P_n, P_0) = \sqrt{(x_n - x_0)^2 + (y_n - y_0)^2} < \varepsilon
$$
由于
$$
|x_n - x_0| \leq \sqrt{(x_n - x_0)^2 + (y_n - y_0)^2} < \varepsilon
$$
因此,$\lim_{n \to \infty} x_n = x_0$。同理可证$\lim_{n \to \infty} y_n = y_0$。
步骤 2:充分性证明
假设$\lim_{n \to \infty} x_n = x_0$和$\lim_{n \to \infty} y_n = y_0$,则对任意给定的正数ε,存在正整数N,当n>N时,有
$$
|x_n - x_0| < \frac{\varepsilon}{\sqrt{2}}
$$
和
$$
|y_n - y_0| < \frac{\varepsilon}{\sqrt{2}}
$$
因此,
$$
\rho(P_n, P_0) = \sqrt{(x_n - x_0)^2 + (y_n - y_0)^2} < \sqrt{\left(\frac{\varepsilon}{\sqrt{2}}\right)^2 + \left(\frac{\varepsilon}{\sqrt{2}}\right)^2} = \varepsilon
$$
所以,点列{Pn(xn,yn)}收敛于P0(x0,y0)。
假设点列{Pn(xn,yn)}收敛于P0(x0,y0),则对任意给定的正数ε,存在正整数N,当n>N时,有
$$
\rho(P_n, P_0) = \sqrt{(x_n - x_0)^2 + (y_n - y_0)^2} < \varepsilon
$$
由于
$$
|x_n - x_0| \leq \sqrt{(x_n - x_0)^2 + (y_n - y_0)^2} < \varepsilon
$$
因此,$\lim_{n \to \infty} x_n = x_0$。同理可证$\lim_{n \to \infty} y_n = y_0$。
步骤 2:充分性证明
假设$\lim_{n \to \infty} x_n = x_0$和$\lim_{n \to \infty} y_n = y_0$,则对任意给定的正数ε,存在正整数N,当n>N时,有
$$
|x_n - x_0| < \frac{\varepsilon}{\sqrt{2}}
$$
和
$$
|y_n - y_0| < \frac{\varepsilon}{\sqrt{2}}
$$
因此,
$$
\rho(P_n, P_0) = \sqrt{(x_n - x_0)^2 + (y_n - y_0)^2} < \sqrt{\left(\frac{\varepsilon}{\sqrt{2}}\right)^2 + \left(\frac{\varepsilon}{\sqrt{2}}\right)^2} = \varepsilon
$$
所以,点列{Pn(xn,yn)}收敛于P0(x0,y0)。