题目
已知F(x)是f(x)的原函数,则 (int )_(a)^xf(t+a)dt=[ ] . ].-|||-(A) F(x)-F(a) (B) F(t)-F(a)-|||-(C) F(x+a)-F(x-a) (D) F(x+a)-F(2a)
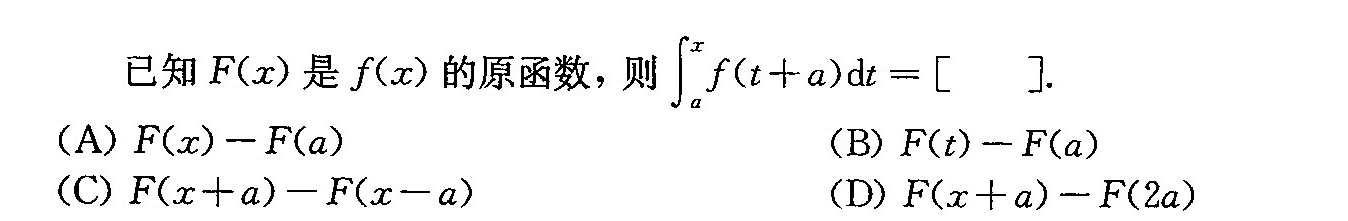
题目解答
答案
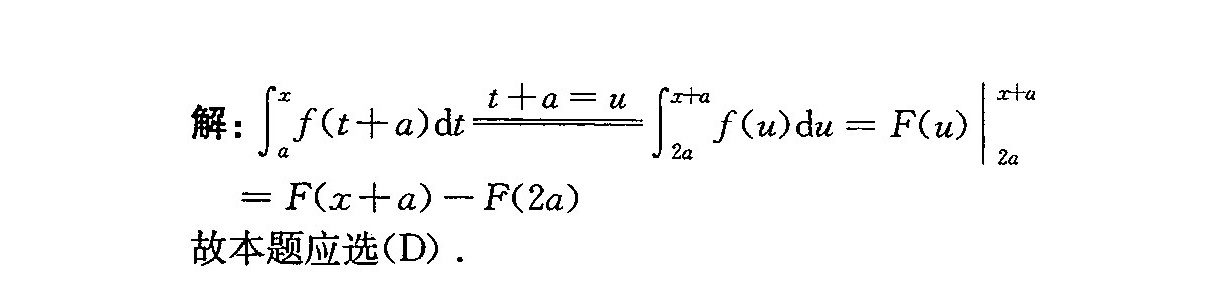
解析
考查要点:本题主要考查定积分的变量替换方法,以及原函数的概念应用。
解题核心思路:通过变量替换将被积函数转化为原函数的形式,利用定积分的计算规则求解。
破题关键点:
- 识别被积函数中的复合结构,即$f(t+a)$,考虑令$u = t + a$进行替换;
- 调整积分上下限,根据变量替换后的表达式确定新上下限;
- 应用原函数的定义,将定积分转化为原函数在上下限处的差值。
变量替换法:
- 令$u = t + a$,则$du = dt$;
- 调整积分上下限:
- 当$t = a$时,$u = a + a = 2a$;
- 当$t = x$时,$u = x + a$;
- 替换积分变量:
$\int_{a}^{x} f(t+a) \, dt = \int_{2a}^{x+a} f(u) \, du$ - 利用原函数计算定积分:
$\int_{2a}^{x+a} f(u) \, du = F(u) \Big|_{2a}^{x+a} = F(x+a) - F(2a)$
选项匹配:结果对应选项(D)。