题目
例28 计算下列积分:-|||-(1) (int )_(0)^2dfrac (x)({e)^x+(e)^2-x}dx ;
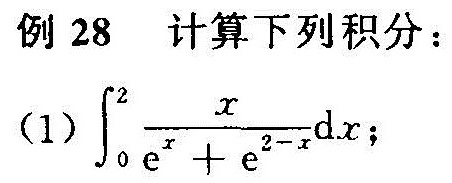
题目解答
答案

解析
步骤 1:分段积分
将积分区间 [0, 2] 分为 [0, 1] 和 [1, 2] 两部分,分别记为 ${I}_{1}$ 和 ${I}_{2}$,即 $I = {I}_{1} + {I}_{2}$。
步骤 2:计算 ${I}_{1}$
${I}_{1} = {\int }_{0}^{1}\dfrac {x}{{e}^{x}+{e}^{2-x}}dx$。
步骤 3:计算 ${I}_{2}$
${I}_{2} = {\int }_{1}^{2}\dfrac {x}{{e}^{x}+{e}^{2-x}}dx$。
步骤 4:利用变量替换
令 $x-2=t$,则 $dx=dt$,${I}_{2}$ 变为 $-{\int }_{0}^{1}\dfrac {x}{{e}^{x}+{e}^{2-x}}dx+{\int }_{1}^{2}\dfrac {2}{{e}^{x}+{e}^{2-x}}dx$。
步骤 5:简化 ${I}_{2}$
${I}_{2} = -{I}_{1} + 2{\int }_{1}^{2}\dfrac {{e}^{x}dx}{{e}^{2x}+{e}^{2}}$。
步骤 6:计算 ${I}_{2}$
${I}_{2} = -{I}_{1} + 2{\int }_{1}^{2}\dfrac {d{e}^{x}}{{e}^{2x}+{e}^{2}}$。
步骤 7:计算 ${I}_{2}$
${I}_{2} = -{I}_{1} + \dfrac {2}{e}(\arctan e - \dfrac {\pi }{4})$。
步骤 8:计算 $I$
$I = {I}_{1} + {I}_{2} = {I}_{1} - {I}_{1} + \dfrac {2}{e}(\arctan e - \dfrac {\pi }{4})$。
将积分区间 [0, 2] 分为 [0, 1] 和 [1, 2] 两部分,分别记为 ${I}_{1}$ 和 ${I}_{2}$,即 $I = {I}_{1} + {I}_{2}$。
步骤 2:计算 ${I}_{1}$
${I}_{1} = {\int }_{0}^{1}\dfrac {x}{{e}^{x}+{e}^{2-x}}dx$。
步骤 3:计算 ${I}_{2}$
${I}_{2} = {\int }_{1}^{2}\dfrac {x}{{e}^{x}+{e}^{2-x}}dx$。
步骤 4:利用变量替换
令 $x-2=t$,则 $dx=dt$,${I}_{2}$ 变为 $-{\int }_{0}^{1}\dfrac {x}{{e}^{x}+{e}^{2-x}}dx+{\int }_{1}^{2}\dfrac {2}{{e}^{x}+{e}^{2-x}}dx$。
步骤 5:简化 ${I}_{2}$
${I}_{2} = -{I}_{1} + 2{\int }_{1}^{2}\dfrac {{e}^{x}dx}{{e}^{2x}+{e}^{2}}$。
步骤 6:计算 ${I}_{2}$
${I}_{2} = -{I}_{1} + 2{\int }_{1}^{2}\dfrac {d{e}^{x}}{{e}^{2x}+{e}^{2}}$。
步骤 7:计算 ${I}_{2}$
${I}_{2} = -{I}_{1} + \dfrac {2}{e}(\arctan e - \dfrac {\pi }{4})$。
步骤 8:计算 $I$
$I = {I}_{1} + {I}_{2} = {I}_{1} - {I}_{1} + \dfrac {2}{e}(\arctan e - \dfrac {\pi }{4})$。