题目
设a,b, in R 证明: ^2+(b)^2+(c)^2=ab+ac+bc 的充要条件是 =b=c.
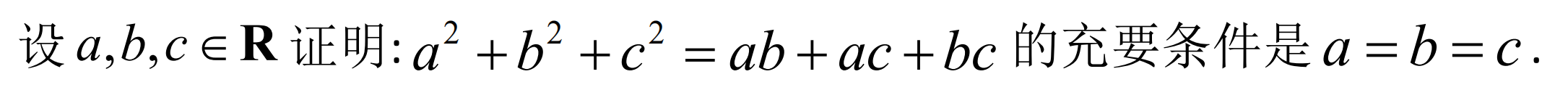
题目解答
答案

解析
步骤 1:充分性证明
假设 $a=b=c$,则有:
\[
{(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}=0
\]
因为 $a=b=c$,所以 $(a-b)=0$,$(b-c)=0$,$(a-c)=0$,从而:
\[
{(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}=0+0+0=0
\]
因此:
\[
{a}^{2}+{b}^{2}+{c}^{2}-ab-ac-bc=0
\]
即:
\[
{a}^{2}+{b}^{2}+{c}^{2}=ab+ac+bc
\]
步骤 2:必要性证明
假设 ${a}^{2}+{b}^{2}+{c}^{2}=ab+ac+bc$,则有:
\[
{a}^{2}+{b}^{2}+{c}^{2}-ab-ac-bc=0
\]
将上式变形为:
\[
\frac{1}{2} \left(2{a}^{2}+2{b}^{2}+2{c}^{2}-2ab-2ac-2bc\right)=0
\]
即:
\[
\frac{1}{2} \left({(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}\right)=0
\]
因为 ${(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}$ 是非负的,所以:
\[
{(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}=0
\]
从而:
\[
a-b=0, b-c=0, a-c=0
\]
即:
\[
a=b=c
\]
假设 $a=b=c$,则有:
\[
{(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}=0
\]
因为 $a=b=c$,所以 $(a-b)=0$,$(b-c)=0$,$(a-c)=0$,从而:
\[
{(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}=0+0+0=0
\]
因此:
\[
{a}^{2}+{b}^{2}+{c}^{2}-ab-ac-bc=0
\]
即:
\[
{a}^{2}+{b}^{2}+{c}^{2}=ab+ac+bc
\]
步骤 2:必要性证明
假设 ${a}^{2}+{b}^{2}+{c}^{2}=ab+ac+bc$,则有:
\[
{a}^{2}+{b}^{2}+{c}^{2}-ab-ac-bc=0
\]
将上式变形为:
\[
\frac{1}{2} \left(2{a}^{2}+2{b}^{2}+2{c}^{2}-2ab-2ac-2bc\right)=0
\]
即:
\[
\frac{1}{2} \left({(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}\right)=0
\]
因为 ${(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}$ 是非负的,所以:
\[
{(a-b)}^{2}+{(b-c)}^{2}+{(a-c)}^{2}=0
\]
从而:
\[
a-b=0, b-c=0, a-c=0
\]
即:
\[
a=b=c
\]