题目
31. lim _(narrow infty )(dfrac (1)({n)^2+n+1}+dfrac (2)({n)^2+n+2}+... +dfrac (n)({n)^2+n+n})=
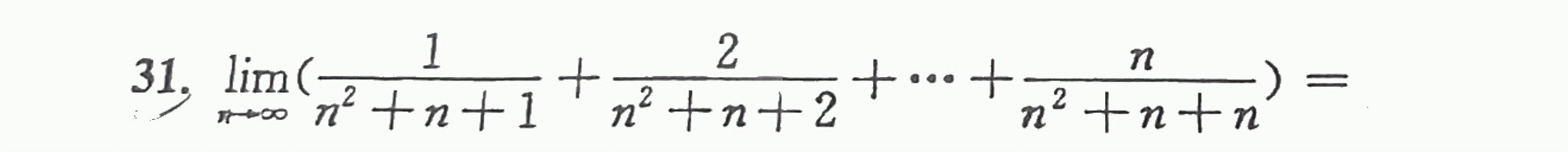
题目解答
答案
解析】
$\lim _{n\rightarrow \infty }(\dfrac {1}{{n}^{2}+n+1}+\dfrac {2}{{n}^{2}+n+2}+\cdots +\dfrac {n}{{n}^{2}+n+n})$
$=\lim _{n\rightarrow \infty }\dfrac {1+2+\cdots +n}{{n}^{2}+n+1+2+2+\cdots +n}$
$=\lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{{n}^{2}+n(n+1)}$
$=\lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{\dfrac {n(n+1)}{2}\cdot 2}$
$=\dfrac {1}{2}$
$\dfrac {1}{2}$
$\lim _{n\rightarrow \infty }(\dfrac {1}{{n}^{2}+n+1}+\dfrac {2}{{n}^{2}+n+2}+\cdots +\dfrac {n}{{n}^{2}+n+n})$
$=\lim _{n\rightarrow \infty }\dfrac {1+2+\cdots +n}{{n}^{2}+n+1+2+2+\cdots +n}$
$=\lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{{n}^{2}+n(n+1)}$
$=\lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{\dfrac {n(n+1)}{2}\cdot 2}$
$=\dfrac {1}{2}$
$\dfrac {1}{2}$
解析
考查要点:本题主要考查数列极限的求解方法,特别是处理分式求和的极限问题。关键在于合理近似分母或利用夹逼定理简化计算。
解题思路:
当$n$趋向于无穷大时,分母中的$n^2$项占主导地位。可以将每个分式中的分母近似为$n^2$,从而将求和转化为等差数列求和。进一步通过夹逼定理严格证明极限值。
破题关键:
- 分母近似:当$n$很大时,$n^2 + n + k \approx n^2$。
- 求和简化:分子为$1+2+\cdots+n = \frac{n(n+1)}{2}$,分母近似为$n \cdot n^2 = n^3$。
- 极限化简:整体表达式近似为$\frac{n^2}{2n^3} = \frac{1}{2n} \to \frac{1}{2}$。
步骤1:观察分母结构
每个分式的分母为$n^2 + n + k$,当$n$很大时,$n^2$是主导项,因此分母近似为$n^2$。
步骤2:近似求和
将原式近似为:
$\sum_{k=1}^{n} \frac{k}{n^2} = \frac{1}{n^2} \sum_{k=1}^{n} k = \frac{1}{n^2} \cdot \frac{n(n+1)}{2} = \frac{n+1}{2n} \to \frac{1}{2} \quad (n \to \infty)$
步骤3:严格证明(夹逼定理)
- 下界:分母$n^2 + n + k \leq n^2 + 2n$,故
$\sum_{k=1}^{n} \frac{k}{n^2 + 2n} = \frac{n(n+1)/2}{n^2 + 2n} = \frac{n+1}{2(n + 2)} \to \frac{1}{2}$ - 上界:分母$n^2 + n + k \geq n^2 + n + 1$,故
$\sum_{k=1}^{n} \frac{k}{n^2 + n + 1} = \frac{n(n+1)/2}{n^2 + n + 1} = \frac{n+1}{2(n + 1 + \frac{1}{n})} \to \frac{1}{2}$
由夹逼定理,极限为$\frac{1}{2}$。