题目
若向量组_(1),(X)_(2),(X)_(3)线性无关,则_(1),(X)_(2),(X)_(3)。A.对B.错
若向量组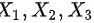 线性无关,则
线性无关,则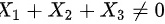 。
。
A.对
B.错
题目解答
答案
解:
根据向量组线性无关的定义,题目中向量组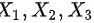 线性无关,即是只有当
线性无关,即是只有当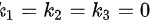 时,才有
时,才有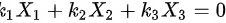 ,而题目中
,而题目中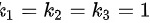 ,故
,故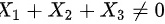
解析
考查要点:本题主要考查向量组线性无关的定义及其应用,需要理解线性无关与线性组合的关系。
解题核心思路:
向量组线性无关的定义是仅当所有系数为零时,其线性组合才等于零向量。若存在非零系数使得线性组合为零向量,则向量组线性相关。题目中给出向量组线性无关,需判断特定线性组合是否可能为零向量。
破题关键点:
通过构造反例,说明存在线性无关的向量组,其系数均为1时线性组合为零向量,从而推翻原命题。
反例构造:
设向量组 $X_1 = \begin{pmatrix}1\\1\\0\end{pmatrix}$,$X_2 = \begin{pmatrix}1\\0\\1\end{pmatrix}$,$X_3 = \begin{pmatrix}-2\\-1\\-1\end{pmatrix}$,验证其线性无关性:
-
线性组合方程:
$aX_1 + bX_2 + cX_3 = \begin{pmatrix}a + b - 2c \\ a - c \\ b - c\end{pmatrix} = \begin{pmatrix}0\\0\\0\end{pmatrix}$ -
解方程组:
- 由第三行得 $b = c$,第二行得 $a = c$,代入第一行得 $c + c - 2c = 0$,恒成立。
- 唯一解为 $a = b = c = 0$,故向量组线性无关。
-
验证和为零向量:
$X_1 + X_2 + X_3 = \begin{pmatrix}1+1-2\\1+0-1\\0+1-1\end{pmatrix} = \begin{pmatrix}0\\0\\0\end{pmatrix}$
结论:存在线性无关的向量组,其和为零向量,故原命题错误。