题目
求下列参数方程所确定的函数的二阶导数 dfrac ({d)^2y}(d{x)^2}-|||-(1) { , y=1-t . 设f"(t)存在且不为零.

题目解答
答案
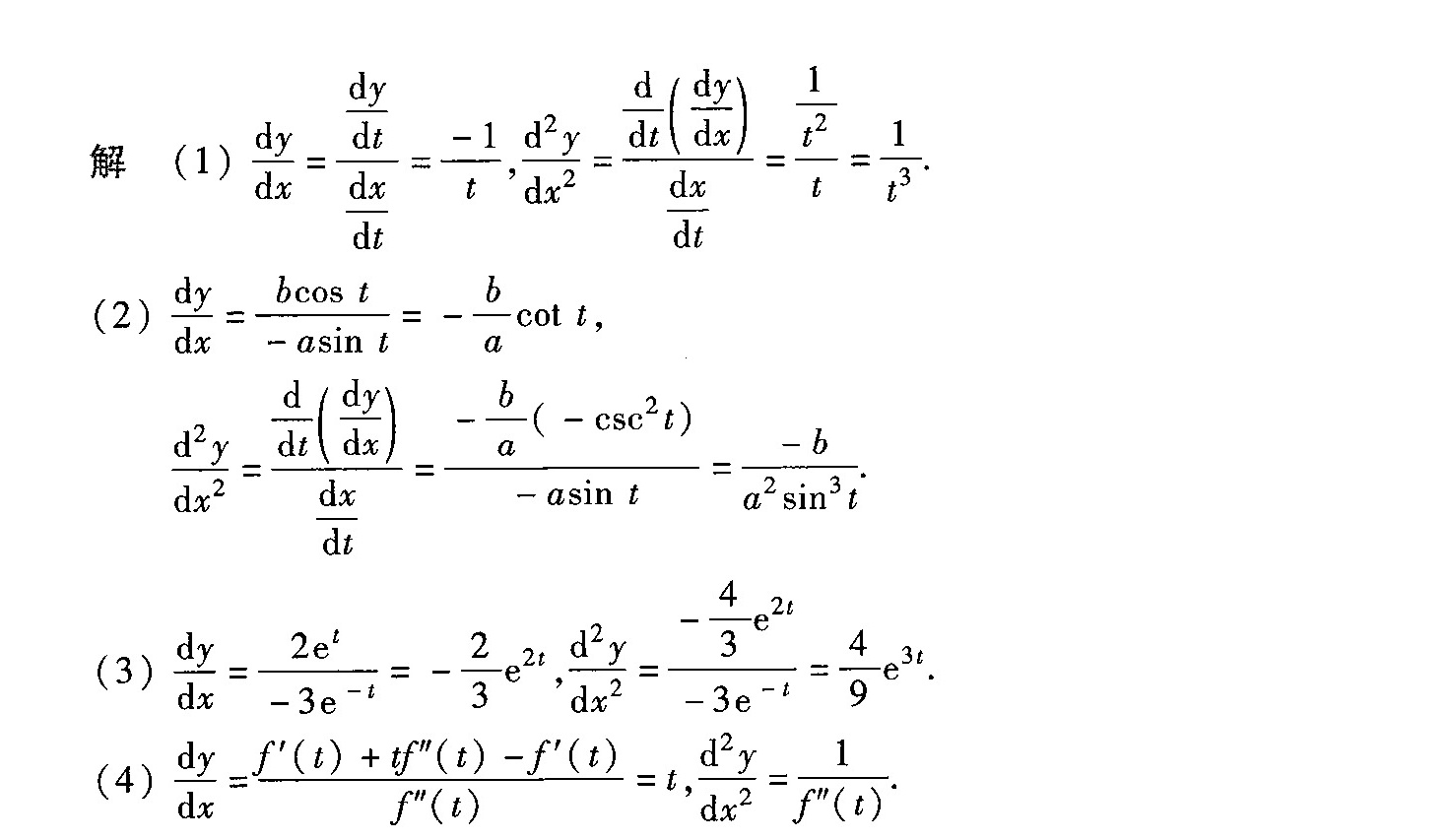
解析
步骤 1:计算 $\dfrac{dy}{dx}$
对于参数方程,我们首先需要计算 $\dfrac{dy}{dx}$,这可以通过 $\dfrac{dy}{dx} = \dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$ 来实现。
步骤 2:计算 $\dfrac{d^2y}{dx^2}$
在得到 $\dfrac{dy}{dx}$ 后,我们再计算 $\dfrac{d^2y}{dx^2}$,这可以通过 $\dfrac{d^2y}{dx^2} = \dfrac{\dfrac{d}{dt}(\dfrac{dy}{dx})}{\dfrac{dx}{dt}}$ 来实现。
步骤 3:代入参数方程
将参数方程中的 $x$ 和 $y$ 的表达式代入上述步骤中,计算出 $\dfrac{dy}{dx}$ 和 $\dfrac{d^2y}{dx^2}$。
对于参数方程,我们首先需要计算 $\dfrac{dy}{dx}$,这可以通过 $\dfrac{dy}{dx} = \dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$ 来实现。
步骤 2:计算 $\dfrac{d^2y}{dx^2}$
在得到 $\dfrac{dy}{dx}$ 后,我们再计算 $\dfrac{d^2y}{dx^2}$,这可以通过 $\dfrac{d^2y}{dx^2} = \dfrac{\dfrac{d}{dt}(\dfrac{dy}{dx})}{\dfrac{dx}{dt}}$ 来实现。
步骤 3:代入参数方程
将参数方程中的 $x$ 和 $y$ 的表达式代入上述步骤中,计算出 $\dfrac{dy}{dx}$ 和 $\dfrac{d^2y}{dx^2}$。