题目
计算曲面:z=-x 2-|||--y^2上点:z=-x 2-|||--y^2处的切平面以及该切平面在第一卦限部分的面积.
计算曲面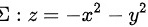
上点
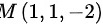处的切平面以及该切平面在第一卦限部分的面积.
题目解答
答案
题目已知曲面方程为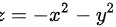
则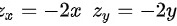
将点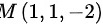代入偏导
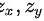可得：
切平面法向量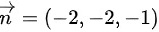
于是切平面方程为：
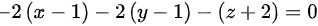
化简可得：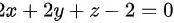
令对应变量为零可得：
切平面在坐标轴
的交点分别为：
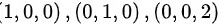
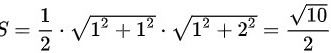
故答案为：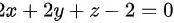
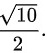
解析
步骤 1：求偏导数
给定曲面方程为$z=-{x}^{2}-{y}^{2}$，我们首先需要求出该曲面在点M(1,1,-2)处的偏导数。偏导数${z}_{x}$和${z}_{y}$分别表示曲面在x和y方向上的变化率。
步骤 2：计算偏导数
计算偏导数${z}_{x}=-2x$和${z}_{y}=-2y$。将点M(1,1,-2)的坐标代入，得到${z}_{x}=-2$和${z}_{y}=-2$。
步骤 3：确定切平面方程
切平面的法向量$\overrightarrow {n}$由偏导数确定，即$\overrightarrow {n}=(-2,-2,-1)$。利用点M(1,1,-2)和法向量$\overrightarrow {n}$，可以写出切平面方程：$-2(x-1)-2(y-1)-(z+2)=0$。化简得到切平面方程为$2x+2y+z-2=0$。
步骤 4：计算切平面在第一卦限部分的面积
切平面在第一卦限部分的面积可以通过计算切平面与坐标轴的交点来确定。令$x=0$，$y=0$，$z=0$，分别求出切平面与坐标轴的交点。交点分别为(1,0,0)，(0,1,0)，(0,0,2)。利用这些交点，可以计算出切平面在第一卦限部分的面积$S=\dfrac {1}{2}\cdot \sqrt {{1}^{2}+{1}^{2}}\cdot \sqrt {{1}^{2}+{2}^{2}}=\dfrac {\sqrt {10}}{2}$。
给定曲面方程为$z=-{x}^{2}-{y}^{2}$，我们首先需要求出该曲面在点M(1,1,-2)处的偏导数。偏导数${z}_{x}$和${z}_{y}$分别表示曲面在x和y方向上的变化率。
步骤 2：计算偏导数
计算偏导数${z}_{x}=-2x$和${z}_{y}=-2y$。将点M(1,1,-2)的坐标代入，得到${z}_{x}=-2$和${z}_{y}=-2$。
步骤 3：确定切平面方程
切平面的法向量$\overrightarrow {n}$由偏导数确定，即$\overrightarrow {n}=(-2,-2,-1)$。利用点M(1,1,-2)和法向量$\overrightarrow {n}$，可以写出切平面方程：$-2(x-1)-2(y-1)-(z+2)=0$。化简得到切平面方程为$2x+2y+z-2=0$。
步骤 4：计算切平面在第一卦限部分的面积
切平面在第一卦限部分的面积可以通过计算切平面与坐标轴的交点来确定。令$x=0$，$y=0$，$z=0$，分别求出切平面与坐标轴的交点。交点分别为(1,0,0)，(0,1,0)，(0,0,2)。利用这些交点，可以计算出切平面在第一卦限部分的面积$S=\dfrac {1}{2}\cdot \sqrt {{1}^{2}+{1}^{2}}\cdot \sqrt {{1}^{2}+{2}^{2}}=\dfrac {\sqrt {10}}{2}$。