题目
15.设 lt (x)_(1)lt 3, _(n+1)=sqrt ({x)_(n)(3-(x)_(n))}(n=1,2,... ), 证明:数列(xn)的极限存在,并求此-|||-极限.
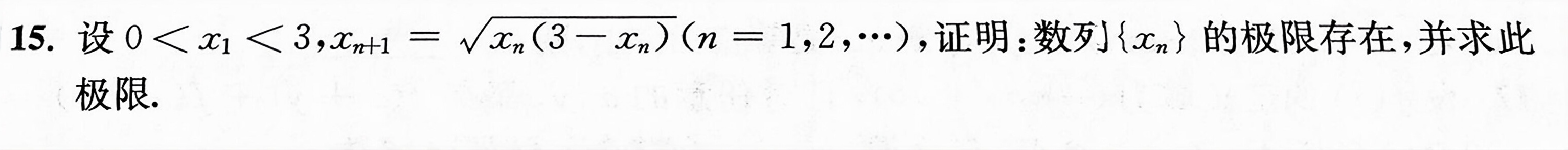
题目解答
答案

解析
步骤 1:证明数列{xn}有界
由 $0\lt {x}_{1}\lt 3$ ,知x1, $3-{x}_{1}$ 均为正数,故 $0\lt {x}_{2}=\sqrt {{x}_{1}(3-{x}_{1})}$ $\leqslant \dfrac {1}{2}({x}_{1}+3-{x}_{1})=\dfrac {3}{2}$ . 设 $0\lt {x}_{k}\leqslant \dfrac {3}{2}(k\gt 1)$ ,则 $0\lt {x}_{k+1}=$ $\sqrt {{x}_{k}(3-{x}_{k})}\leqslant \dfrac {1}{2}({x}_{k}+3-{x}_{k})=\dfrac {3}{2}$ 由数学归纳法知,对任意正整数 $n\gt 1$ 均有 $0\lt {x}_{n}\leqslant \dfrac {3}{2}$ ,因而数列{xn}有界.
步骤 2:证明数列{xn}单调增加
当 $n\gt 1$ 时, ${x}_{n+1}-{x}_{n}=\sqrt {{x}_{n}(3-{x}_{n})}-{x}_{n}$ =√x $\overline {m}(\sqrt {3-{x}_{n}}-\sqrt {{x}_{n}})=\dfrac {\sqrt {{x}_{n}(3-2{x}_{n})}^{2}}{\sqrt {3-{x}_{n}}+\sqrt {{x}_{n}}}$ $\geqslant 0$ . 因而有 ${x}_{n+1}\geqslant {x}_{n}(n\gt 1)$ ,即数列{xn}单调增加.
步骤 3:求极限
由单调有界数列必有极限,知limxn存在. 设 $\lim {x}_{n}=a$ ,在 ${x}_{n+1}=\sqrt {{x}_{n}(3-{x}_{n})}$ 两边取极限,得 $a=\sqrt {a(3-a)}$ ,则 $a=\dfrac {3}{2}$ ,a=0 (舍去). 故 $\lim _{n\rightarrow \infty }{x}_{n}=\dfrac {3}{2}$
由 $0\lt {x}_{1}\lt 3$ ,知x1, $3-{x}_{1}$ 均为正数,故 $0\lt {x}_{2}=\sqrt {{x}_{1}(3-{x}_{1})}$ $\leqslant \dfrac {1}{2}({x}_{1}+3-{x}_{1})=\dfrac {3}{2}$ . 设 $0\lt {x}_{k}\leqslant \dfrac {3}{2}(k\gt 1)$ ,则 $0\lt {x}_{k+1}=$ $\sqrt {{x}_{k}(3-{x}_{k})}\leqslant \dfrac {1}{2}({x}_{k}+3-{x}_{k})=\dfrac {3}{2}$ 由数学归纳法知,对任意正整数 $n\gt 1$ 均有 $0\lt {x}_{n}\leqslant \dfrac {3}{2}$ ,因而数列{xn}有界.
步骤 2:证明数列{xn}单调增加
当 $n\gt 1$ 时, ${x}_{n+1}-{x}_{n}=\sqrt {{x}_{n}(3-{x}_{n})}-{x}_{n}$ =√x $\overline {m}(\sqrt {3-{x}_{n}}-\sqrt {{x}_{n}})=\dfrac {\sqrt {{x}_{n}(3-2{x}_{n})}^{2}}{\sqrt {3-{x}_{n}}+\sqrt {{x}_{n}}}$ $\geqslant 0$ . 因而有 ${x}_{n+1}\geqslant {x}_{n}(n\gt 1)$ ,即数列{xn}单调增加.
步骤 3:求极限
由单调有界数列必有极限,知limxn存在. 设 $\lim {x}_{n}=a$ ,在 ${x}_{n+1}=\sqrt {{x}_{n}(3-{x}_{n})}$ 两边取极限,得 $a=\sqrt {a(3-a)}$ ,则 $a=\dfrac {3}{2}$ ,a=0 (舍去). 故 $\lim _{n\rightarrow \infty }{x}_{n}=\dfrac {3}{2}$