题目
22.设 (x,y,z)=(x)^2+2(y)^2+3(z)^2+xy+3x-2y-6z grad f(1,1,1).
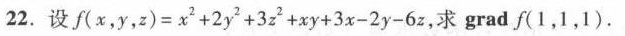
题目解答
答案
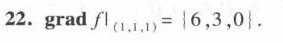
解析
步骤 1:计算偏导数
首先,我们需要计算函数 $f(x,y,z)={x}^{2}+2{y}^{2}+3{z}^{2}+xy+3x-2y-6z$ 关于 $x$、$y$ 和 $z$ 的偏导数。
- 对于 $x$ 的偏导数:$\frac{\partial f}{\partial x} = 2x + y + 3$
- 对于 $y$ 的偏导数:$\frac{\partial f}{\partial y} = 4y + x - 2$
- 对于 $z$ 的偏导数:$\frac{\partial f}{\partial z} = 6z - 6$
步骤 2:计算梯度
梯度 $\nabla f$ 是一个向量,其分量是函数 $f$ 关于每个变量的偏导数。因此,$\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)$。
步骤 3:代入点 (1,1,1)
将点 (1,1,1) 代入梯度的分量中,得到:
- $\frac{\partial f}{\partial x}(1,1,1) = 2(1) + 1 + 3 = 6$
- $\frac{\partial f}{\partial y}(1,1,1) = 4(1) + 1 - 2 = 3$
- $\frac{\partial f}{\partial z}(1,1,1) = 6(1) - 6 = 0$
首先,我们需要计算函数 $f(x,y,z)={x}^{2}+2{y}^{2}+3{z}^{2}+xy+3x-2y-6z$ 关于 $x$、$y$ 和 $z$ 的偏导数。
- 对于 $x$ 的偏导数:$\frac{\partial f}{\partial x} = 2x + y + 3$
- 对于 $y$ 的偏导数:$\frac{\partial f}{\partial y} = 4y + x - 2$
- 对于 $z$ 的偏导数:$\frac{\partial f}{\partial z} = 6z - 6$
步骤 2:计算梯度
梯度 $\nabla f$ 是一个向量,其分量是函数 $f$ 关于每个变量的偏导数。因此,$\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)$。
步骤 3:代入点 (1,1,1)
将点 (1,1,1) 代入梯度的分量中,得到:
- $\frac{\partial f}{\partial x}(1,1,1) = 2(1) + 1 + 3 = 6$
- $\frac{\partial f}{\partial y}(1,1,1) = 4(1) + 1 - 2 = 3$
- $\frac{\partial f}{\partial z}(1,1,1) = 6(1) - 6 = 0$