)设当 arrow 0 时, (1-cos x)ln (1+(x)^2) 是比xsinx"高阶的无穷小,而 xsinx"是比 ((e)^(x^2)-1)-|||-高阶的无穷小,则正整数 n 等于 ()-|||-(A)1 (B)2 (C)3 (D) 4

题目解答
答案
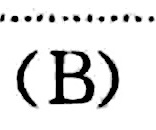
解析
考查要点:本题主要考查无穷小比较的阶数判断,需要利用泰勒展开式或等价无穷小进行分析。
解题核心思路:
- 比较两个无穷小的阶数:当$x \to 0$时,若$f(x)$是$g(x)$的高阶无穷小,则$\lim_{x \to 0} \frac{f(x)}{g(x)} = 0$。
- 展开关键函数:将题目中的函数(如$\cos x$、$\ln(1+x^2)$、$\sin x$、$e^{x^2}-1$)展开为泰勒多项式,提取主要项。
- 确定阶数关系:根据展开式中最高次项的次数,建立关于$n$的不等式,最终确定$n$的值。
破题关键点:
- 第一个条件:$(1-\cos x)\ln(1+x^2)$的阶数高于$x(\sin x)^n$,需通过展开式比较两者的最高次项次数。
- 第二个条件:$x(\sin x)^n$的阶数高于$e^{x^2}-1$,需验证展开后的次数关系。
步骤1:展开各函数的主要项
-
$1 - \cos x$:
$\cos x = 1 - \frac{x^2}{2} + \frac{x^4}{24} - \dots$,故
$1 - \cos x \sim \frac{x^2}{2} \quad (\text{阶数为2})$ -
$\ln(1+x^2)$:
$\ln(1+t) \sim t$(当$t \to 0$),故
$\ln(1+x^2) \sim x^2 \quad (\text{阶数为2})$ -
$(1-\cos x)\ln(1+x^2)$:
两式相乘得:
$\frac{x^2}{2} \cdot x^2 = \frac{x^4}{2} \quad (\text{阶数为4})$ -
$x(\sin x)^n$:
$\sin x \sim x - \frac{x^3}{6} + \dots$,故$(\sin x)^n \sim x^n - \frac{n x^{n+2}}{6} + \dots$,因此:
$x(\sin x)^n \sim x^{n+1} \quad (\text{阶数为}n+1)$ -
$e^{x^2} - 1$:
$e^{x^2} - 1 \sim x^2 + \frac{x^4}{2} + \dots \quad (\text{阶数为2})$
步骤2:建立阶数关系
-
第一个条件:
$(1-\cos x)\ln(1+x^2)$的阶数(4)高于$x(\sin x)^n$的阶数($n+1$),即:
$4 > n+1 \quad \Rightarrow \quad n < 3$ -
第二个条件:
$x(\sin x)^n$的阶数($n+1$)高于$e^{x^2}-1$的阶数(2),即:
$n+1 > 2 \quad \Rightarrow \quad n > 1$
步骤3:确定整数解
综合两个不等式:
$1 < n < 3$
由于$n$为正整数,故$n=2$。