3.问a,b为何值时,有极限-|||-lim _(xarrow 0)(dfrac (sin 3x)({x)^3}+dfrac (a)({x)^2}+b)=0-|||-成立.
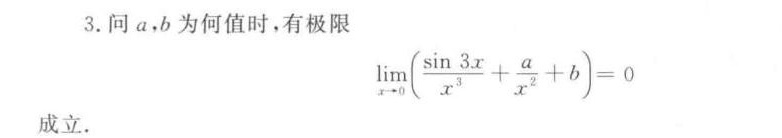
题目解答
答案
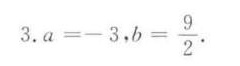
解析
考查要点:本题主要考查极限的计算,特别是利用泰勒展开处理高阶无穷小的叠加问题,以及通过调整参数使极限存在的能力。
解题核心思路:
- 泰勒展开:将$\sin 3x$展开到足够高的阶数,以便分离出不同阶的无穷小项。
- 合并同类项:将展开后的各项与$\frac{a}{x^2}$和$b$合并,分析各阶无穷小的系数。
- 令高阶无穷小系数为零:确保极限存在且为有限值。
- 调整常数项:使剩余常数项等于零,满足极限值为0的条件。
破题关键点:
- 识别高阶无穷小的抵消条件:通过调整$a$和$b$,消除$\frac{1}{x^2}$项的发散性,并使常数项为零。
将$\sin 3x$展开为泰勒级数:
$\sin 3x = 3x - \frac{(3x)^3}{6} + \frac{(3x)^5}{120} - \cdots$
代入原式并拆分项:
$\begin{aligned}\lim_{x \to 0} \left( \frac{\sin 3x}{x^3} + \frac{a}{x^2} + b \right) &= \lim_{x \to 0} \left( \frac{3x - \frac{27x^3}{6} + \cdots}{x^3} + \frac{a}{x^2} + b \right) \\&= \lim_{x \to 0} \left( \frac{3}{x^2} - \frac{9}{2} + \frac{a}{x^2} + b + \cdots \right) \\&= \lim_{x \to 0} \left( \frac{3 + a}{x^2} + \left( b - \frac{9}{2} \right) + \cdots \right)\end{aligned}$
步骤1:消除$\frac{1}{x^2}$项
若$\frac{3 + a}{x^2}$存在,则极限发散。令其系数为零:
$3 + a = 0 \quad \Rightarrow \quad a = -3$
步骤2:调整常数项
剩余常数项为$b - \frac{9}{2}$,令其等于零:
$b - \frac{9}{2} = 0 \quad \Rightarrow \quad b = \frac{9}{2}$