题目
设了为平面了所围成的立体的全表面的外侧,则曲面积分了了
设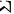 为平面
为平面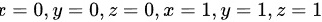 所围成的立体的全表面的外侧,则曲面积分
所围成的立体的全表面的外侧,则曲面积分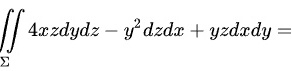
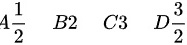
题目解答
答案
由高斯公式,得到: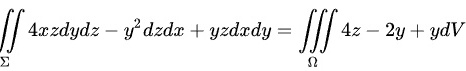
其中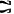 为
为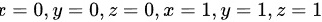 所围成的立体,则
所围成的立体,则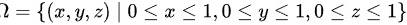
由三重积分的计算方法,得到: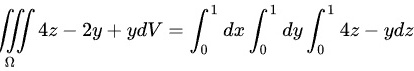
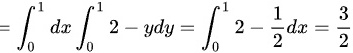
故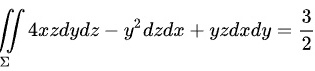
故选择
解析
步骤 1:应用高斯公式
根据高斯公式,曲面积分$\iint 4xzdydz-{y}^{2}dzdx+yzdxdy$可以转化为三重积分$\iiint (4z-2y+y)dV$,其中$V$是立体的体积。
步骤 2:确定积分区域
由题意,立体由平面$x=0,y=0,z=0,x=1,y=1,z=1$围成,因此积分区域$V$为$0\leqslant x\leqslant 1,0\leqslant y\leqslant 1,0\leqslant z\leqslant 1$。
步骤 3:计算三重积分
根据步骤2中的积分区域,计算三重积分$\iiint (4z-2y+y)dV$,即$\int_{0}^{1}dx\int_{0}^{1}dy\int_{0}^{1}(4z-2y+y)dz$。
步骤 4:计算内层积分
首先计算内层积分$\int_{0}^{1}(4z-2y+y)dz$,得到$[2z^2-(2y-y)z]_{0}^{1}=2-(2y-y)=2-y$。
步骤 5:计算中层积分
接下来计算中层积分$\int_{0}^{1}(2-y)dy$,得到$[2y-\frac{1}{2}y^2]_{0}^{1}=2-\frac{1}{2}=\frac{3}{2}$。
步骤 6:计算外层积分
最后计算外层积分$\int_{0}^{1}\frac{3}{2}dx$,得到$\frac{3}{2}x|_{0}^{1}=\frac{3}{2}$。
根据高斯公式,曲面积分$\iint 4xzdydz-{y}^{2}dzdx+yzdxdy$可以转化为三重积分$\iiint (4z-2y+y)dV$,其中$V$是立体的体积。
步骤 2:确定积分区域
由题意,立体由平面$x=0,y=0,z=0,x=1,y=1,z=1$围成,因此积分区域$V$为$0\leqslant x\leqslant 1,0\leqslant y\leqslant 1,0\leqslant z\leqslant 1$。
步骤 3:计算三重积分
根据步骤2中的积分区域,计算三重积分$\iiint (4z-2y+y)dV$,即$\int_{0}^{1}dx\int_{0}^{1}dy\int_{0}^{1}(4z-2y+y)dz$。
步骤 4:计算内层积分
首先计算内层积分$\int_{0}^{1}(4z-2y+y)dz$,得到$[2z^2-(2y-y)z]_{0}^{1}=2-(2y-y)=2-y$。
步骤 5:计算中层积分
接下来计算中层积分$\int_{0}^{1}(2-y)dy$,得到$[2y-\frac{1}{2}y^2]_{0}^{1}=2-\frac{1}{2}=\frac{3}{2}$。
步骤 6:计算外层积分
最后计算外层积分$\int_{0}^{1}\frac{3}{2}dx$,得到$\frac{3}{2}x|_{0}^{1}=\frac{3}{2}$。