21. lim _(xarrow infty )((dfrac {x)(2+x))}^3x
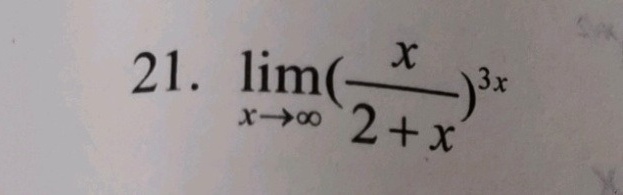
题目解答
答案
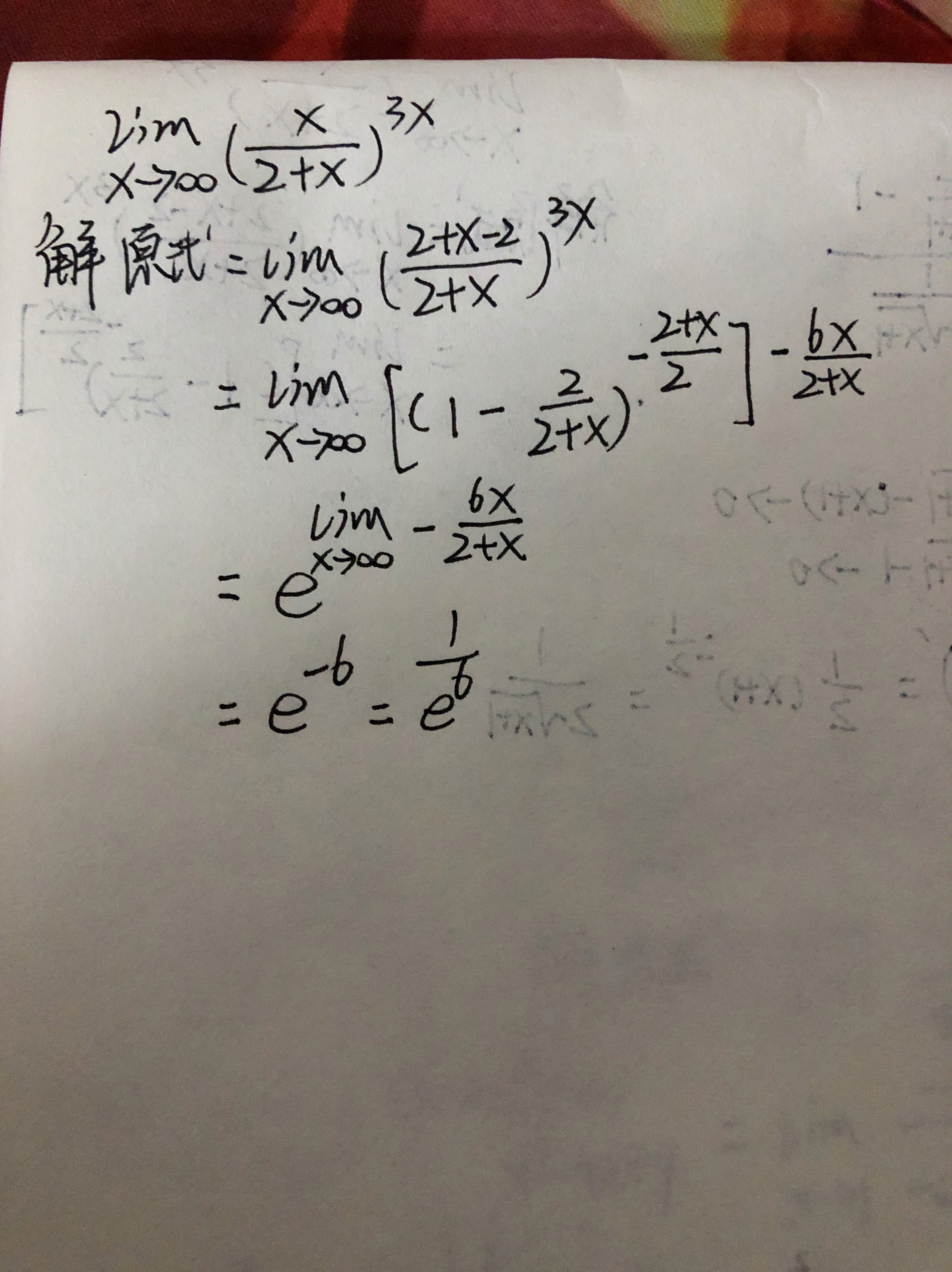
解析
考查要点:本题主要考查极限的计算方法,特别是处理形如$1^\infty$型不定式的极限问题。需要掌握对数转换法和等价无穷小替换的应用。
解题核心思路:
当遇到$\lim_{x \to \infty} f(x)^{g(x)}$且$f(x) \to 1$、$g(x) \to \infty$时,通常通过以下步骤处理:
- 取自然对数,将指数运算转化为乘法;
- 化简表达式,利用等价无穷小替换简化运算;
- 求极限后取指数,得到原式的极限值。
破题关键点:
将$\dfrac{x}{2+x}$变形为$1 - \dfrac{2}{2+x}$,并利用$\ln(1+t) \sim t$(当$t \to 0$时)进行替换。
步骤1:取自然对数
设原式为$L = \lim_{x \to \infty} \left( \dfrac{x}{2+x} \right)^{3x}$,取自然对数得:
$\ln L = \lim_{x \to \infty} 3x \cdot \ln \left( \dfrac{x}{2+x} \right)$
步骤2:化简对数表达式
将$\dfrac{x}{2+x}$变形为$\dfrac{1}{1+\frac{2}{x}}$,则:
$\ln \left( \dfrac{x}{2+x} \right) = \ln \left( \dfrac{1}{1+\frac{2}{x}} \right) = -\ln \left( 1 + \dfrac{2}{x} \right)$
步骤3:应用等价无穷小替换
当$x \to \infty$时,$\dfrac{2}{x} \to 0$,利用$\ln(1+t) \sim t$($t \to 0$),得:
$-\ln \left( 1 + \dfrac{2}{x} \right) \sim -\dfrac{2}{x}$
步骤4:求极限
代入$\ln L$的表达式:
$\ln L = \lim_{x \to \infty} 3x \cdot \left( -\dfrac{2}{x} \right) = \lim_{x \to \infty} (-6) = -6$
步骤5:取指数得结果
原式为:
$L = e^{\ln L} = e^{-6} = \dfrac{1}{e^6}$