题目
求下列函数当 arrow 0 时的左、右极限,并指出当x→0时极限是否-|||-存在.-|||-(x)=dfrac (|x|)(x);

题目解答
答案
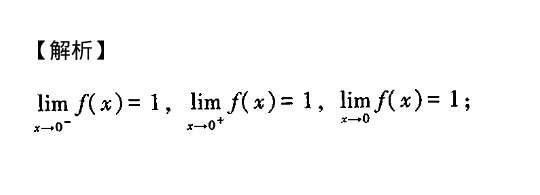
解析
考查要点:本题主要考查分段函数在分段点处的左右极限计算,以及极限存在的条件。
解题核心思路:
- 分段讨论:由于函数$f(x)=\dfrac{|x|}{x}$在$x=0$处无定义,且绝对值函数在$x>0$和$x<0$时的表达式不同,需分别计算左极限($x \to 0^-$)和右极限($x \to 0^+$)。
- 化简表达式:根据$x$的正负性,将绝对值符号展开,化简后求极限。
- 判断极限存在性:若左右极限相等,则极限存在;否则不存在。
破题关键点:
- 绝对值的处理:当$x>0$时,$|x|=x$;当$x<0$时,$|x|=-x$。
- 分母不为零:虽然$x=0$时函数无定义,但极限讨论的是$x$趋近于0的过程,而非$x=0$的函数值。
左极限($x \to 0^-$)
当$x \to 0^-$时,$x$为负数,因此$|x| = -x$。
代入函数得:
$f(x) = \dfrac{|x|}{x} = \dfrac{-x}{x} = -1$
因此,左极限为:
$\lim_{x \to 0^-} f(x) = -1$
右极限($x \to 0^+$)
当$x \to 0^+$时,$x$为正数,因此$|x| = x$。
代入函数得:
$f(x) = \dfrac{|x|}{x} = \dfrac{x}{x} = 1$
因此,右极限为:
$\lim_{x \to 0^+} f(x) = 1$
极限存在性判断
由于左极限($-1$)与右极限($1$)不相等,故当$x \to 0$时,函数$f(x)$的极限不存在。