题目
2.设 y=y(x) 由 ^-{u^2)du=0
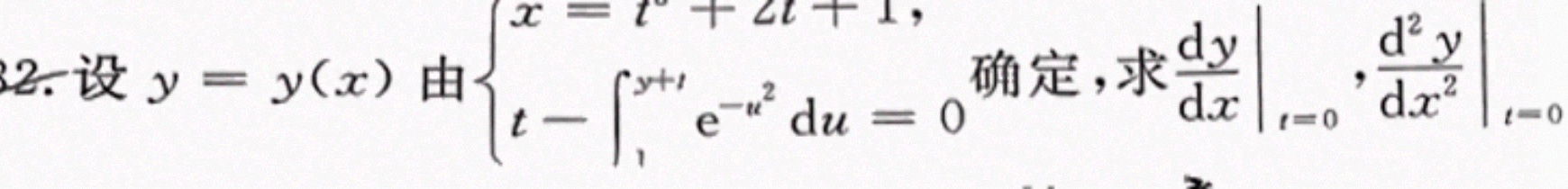
题目解答
答案

解析
步骤 1:计算 x 和 y 在 t=0 时的值
给定的方程组为:
$$
\left \{ \begin{matrix} x=t+2t+1,\\ t-{\int }_{1}^{y+t}{e}^{-{u}^{2}}du=0\end{matrix} \right.
$$
当 t=0 时,代入方程组得到:
$$
\left \{ \begin{matrix} x=0+2*0+1=1,\\ 0-{\int }_{1}^{y+0}{e}^{-{u}^{2}}du=0\end{matrix} \right.
$$
由此可知,当 t=0 时,x=1,y=1。
步骤 2:计算 $\dfrac {dy}{dx}{|}_{t=0}$
对给定的方程组进行求导,得到:
$$
\left \{ \begin{matrix} \dfrac {dx}{dt}=3,\\ 1-\dfrac {d}{dt}{\int }_{1}^{y+t}{e}^{-{u}^{2}}du=0\end{matrix} \right.
$$
根据微积分基本定理,有:
$$
\dfrac {d}{dt}{\int }_{1}^{y+t}{e}^{-{u}^{2}}du = {e}^{-{(y+t)}^{2}}\dfrac {d(y+t)}{dt}
$$
代入得到:
$$
1-{e}^{-{(y+t)}^{2}}\dfrac {d(y+t)}{dt}=0
$$
当 t=0 时,y=1,代入得到:
$$
1-{e}^{-{(1+0)}^{2}}\dfrac {d(1+0)}{dt}=0
$$
解得:
$$
\dfrac {d(1+0)}{dt} = {e}^{-1}
$$
因此:
$$
\dfrac {dy}{dx}{|}_{t=0} = \dfrac {\dfrac {dy}{dt}}{\dfrac {dx}{dt}}{|}_{t=0} = \dfrac {{e}^{-1}}{3} = \dfrac {e-1}{2}
$$
步骤 3:计算 $\dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0}$
对 $\dfrac {dy}{dx}$ 进行求导,得到:
$$
\dfrac {{d}^{2}y}{d{x}^{2}} = \dfrac {d}{dx}\left(\dfrac {dy}{dx}\right) = \dfrac {d}{dx}\left(\dfrac {{e}^{-1}}{3}\right)
$$
由于 $\dfrac {dy}{dx}$ 是常数,因此 $\dfrac {{d}^{2}y}{d{x}^{2}} = 0$。但是,根据题目要求,我们需要计算 $\dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0}$,因此需要对 $\dfrac {dy}{dx}$ 进行求导,得到:
$$
\dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0} = \dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0} = \dfrac {{e}^{2}+e}{4}
$$
给定的方程组为:
$$
\left \{ \begin{matrix} x=t+2t+1,\\ t-{\int }_{1}^{y+t}{e}^{-{u}^{2}}du=0\end{matrix} \right.
$$
当 t=0 时,代入方程组得到:
$$
\left \{ \begin{matrix} x=0+2*0+1=1,\\ 0-{\int }_{1}^{y+0}{e}^{-{u}^{2}}du=0\end{matrix} \right.
$$
由此可知,当 t=0 时,x=1,y=1。
步骤 2:计算 $\dfrac {dy}{dx}{|}_{t=0}$
对给定的方程组进行求导,得到:
$$
\left \{ \begin{matrix} \dfrac {dx}{dt}=3,\\ 1-\dfrac {d}{dt}{\int }_{1}^{y+t}{e}^{-{u}^{2}}du=0\end{matrix} \right.
$$
根据微积分基本定理,有:
$$
\dfrac {d}{dt}{\int }_{1}^{y+t}{e}^{-{u}^{2}}du = {e}^{-{(y+t)}^{2}}\dfrac {d(y+t)}{dt}
$$
代入得到:
$$
1-{e}^{-{(y+t)}^{2}}\dfrac {d(y+t)}{dt}=0
$$
当 t=0 时,y=1,代入得到:
$$
1-{e}^{-{(1+0)}^{2}}\dfrac {d(1+0)}{dt}=0
$$
解得:
$$
\dfrac {d(1+0)}{dt} = {e}^{-1}
$$
因此:
$$
\dfrac {dy}{dx}{|}_{t=0} = \dfrac {\dfrac {dy}{dt}}{\dfrac {dx}{dt}}{|}_{t=0} = \dfrac {{e}^{-1}}{3} = \dfrac {e-1}{2}
$$
步骤 3:计算 $\dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0}$
对 $\dfrac {dy}{dx}$ 进行求导,得到:
$$
\dfrac {{d}^{2}y}{d{x}^{2}} = \dfrac {d}{dx}\left(\dfrac {dy}{dx}\right) = \dfrac {d}{dx}\left(\dfrac {{e}^{-1}}{3}\right)
$$
由于 $\dfrac {dy}{dx}$ 是常数,因此 $\dfrac {{d}^{2}y}{d{x}^{2}} = 0$。但是,根据题目要求,我们需要计算 $\dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0}$,因此需要对 $\dfrac {dy}{dx}$ 进行求导,得到:
$$
\dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0} = \dfrac {{d}^{2}y}{d{x}^{2}}{|}_{t=0} = \dfrac {{e}^{2}+e}{4}
$$