题目
[2.1]当 C= __ 时, X=k =Ccdot ((dfrac {2)(3))}^k(k=1,2,3,... ) 才能成为随机变量X的分布-|||-列.
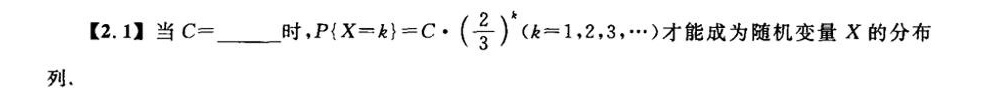
题目解答
答案

解析
关键知识点:本题考查概率分布列的性质,特别是所有概率之和等于1的条件。需要利用无穷等比数列求和公式求解常数C的值。
解题思路:
- 根据分布列的性质,所有概率之和必须等于1。
- 将给定的概率表达式代入求和公式,转化为等比数列求和问题。
- 利用等比数列求和公式计算总和,解方程求出C的值。
步骤1:列出概率和为1的方程
根据分布列的性质,所有概率之和为1:
$\sum_{k=1}^{\infty} C \cdot \left( \dfrac{2}{3} \right)^k = 1$
步骤2:识别等比数列结构
该级数是首项为$C \cdot \dfrac{2}{3}$、公比为$\dfrac{2}{3}$的无穷等比数列。其和公式为:
$\text{和} = \dfrac{\text{首项}}{1 - \text{公比}} = \dfrac{C \cdot \dfrac{2}{3}}{1 - \dfrac{2}{3}}$
步骤3:代入公式并解方程
计算分母:
$1 - \dfrac{2}{3} = \dfrac{1}{3}$
代入公式得:
$C \cdot \dfrac{\dfrac{2}{3}}{\dfrac{1}{3}} = C \cdot 2 = 1$
解得:
$C = \dfrac{1}{2}$