题目
计算 iint dfrac (sin y)(y)dxdy, 其中D是由直-|||-线 y=x 及抛物线 ^2=x 所围成的闭区域.
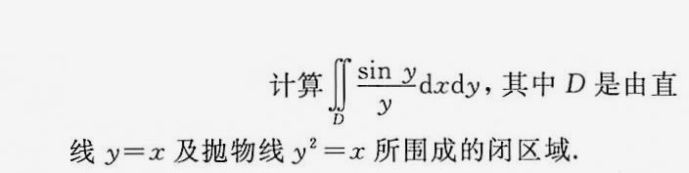
题目解答
答案
解析
步骤 1:确定积分区域D
D是由直线y=x和抛物线${y}^{2}=x$所围成的闭区域。首先,我们需要确定这两个曲线的交点。将y=x代入${y}^{2}=x$,得到${x}^{2}=x$,解得x=0或x=1。因此,交点为(0,0)和(1,1)。所以,D是一个在x=0到x=1之间,y从${y}^{2}=x$到y=x的区域。
步骤 2:选择积分顺序
由于D既是一个X型区域也是一个Y型区域,我们可以选择先对x积分后对y积分。这样,积分区域D可以表示为$0\leq y\leq 1$,${y}^{2}\leq x\leq y$。
步骤 3:计算二重积分
根据步骤2,我们有:
$\iint \dfrac {\sin y}{y}dxdy={\int }_{0}^{1}dy{\int }_{{y}^{2}}^{y}\dfrac {\sin y}{y}dx$。
先对x积分,得到:
${\int }_{{y}^{2}}^{y}\dfrac {\sin y}{y}dx=\dfrac {\sin y}{y}[x]_{{y}^{2}}^{y}=\dfrac {\sin y}{y}(y-{y}^{2})=(1-y)\sin y$。
然后对y积分,得到:
${\int }_{0}^{1}(1-y)\sin ydy$。
利用分部积分法,设$u=1-y$,$dv=\sin ydy$,则$du=-dy$,$v=-\cos y$。因此,原积分变为:
${\int }_{0}^{1}(1-y)\sin ydy=[-(1-y)\cos y]_{0}^{1}-{\int }_{0}^{1}\cos ydy$。
计算得:
$=[-(1-1)\cos 1+(1-0)\cos 0]-[\sin y]_{0}^{1}=1-\sin 1$。
D是由直线y=x和抛物线${y}^{2}=x$所围成的闭区域。首先,我们需要确定这两个曲线的交点。将y=x代入${y}^{2}=x$,得到${x}^{2}=x$,解得x=0或x=1。因此,交点为(0,0)和(1,1)。所以,D是一个在x=0到x=1之间,y从${y}^{2}=x$到y=x的区域。
步骤 2:选择积分顺序
由于D既是一个X型区域也是一个Y型区域,我们可以选择先对x积分后对y积分。这样,积分区域D可以表示为$0\leq y\leq 1$,${y}^{2}\leq x\leq y$。
步骤 3:计算二重积分
根据步骤2,我们有:
$\iint \dfrac {\sin y}{y}dxdy={\int }_{0}^{1}dy{\int }_{{y}^{2}}^{y}\dfrac {\sin y}{y}dx$。
先对x积分,得到:
${\int }_{{y}^{2}}^{y}\dfrac {\sin y}{y}dx=\dfrac {\sin y}{y}[x]_{{y}^{2}}^{y}=\dfrac {\sin y}{y}(y-{y}^{2})=(1-y)\sin y$。
然后对y积分,得到:
${\int }_{0}^{1}(1-y)\sin ydy$。
利用分部积分法,设$u=1-y$,$dv=\sin ydy$,则$du=-dy$,$v=-\cos y$。因此,原积分变为:
${\int }_{0}^{1}(1-y)\sin ydy=[-(1-y)\cos y]_{0}^{1}-{\int }_{0}^{1}\cos ydy$。
计算得:
$=[-(1-1)\cos 1+(1-0)\cos 0]-[\sin y]_{0}^{1}=1-\sin 1$。