题目
设:(x)^2+(y)^2=(a)^2 是正向闭曲线,计算曲线积分 :(x)^2+(y)^2=(a)^2
设 是正向闭曲线,计算曲线积分
是正向闭曲线,计算曲线积分 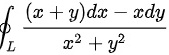
题目解答
答案
由题意,已知
 是正向闭曲线
是正向闭曲线
∴曲线积分 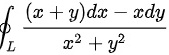
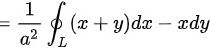
令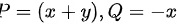
则,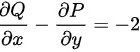
∴根据格林公式,得
曲线积分 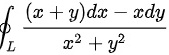
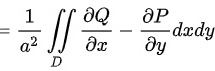
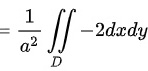
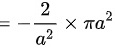

解析
步骤 1:确定曲线积分的被积函数
曲线积分的被积函数为 $\dfrac {(x+y)dx-xdy}{{x}^{2}+{y}^{2}}$,其中 $C$ 是正向闭曲线,即 $C:{x}^{2}+{y}^{2}={a}^{2}$。
步骤 2:应用格林公式
格林公式指出,对于一个闭合曲线 $C$ 上的曲线积分,如果 $P(x,y)$ 和 $Q(x,y)$ 在 $C$ 内部的区域 $D$ 上具有连续的一阶偏导数,则有
$$\oint_C Pdx + Qdy = \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dxdy$$
其中,$P(x,y) = \frac{x+y}{{x}^{2}+{y}^{2}}$,$Q(x,y) = -\frac{x}{{x}^{2}+{y}^{2}}$。
步骤 3:计算偏导数
计算 $\frac{\partial Q}{\partial x}$ 和 $\frac{\partial P}{\partial y}$:
$$\frac{\partial Q}{\partial x} = -\frac{{x}^{2}+{y}^{2} - 2x^2}{{({x}^{2}+{y}^{2})}^{2}} = -\frac{{y}^{2}-{x}^{2}}{{({x}^{2}+{y}^{2})}^{2}}$$
$$\frac{\partial P}{\partial y} = \frac{{x}^{2}+{y}^{2} - 2y^2}{{({x}^{2}+{y}^{2})}^{2}} = \frac{{x}^{2}-{y}^{2}}{{({x}^{2}+{y}^{2})}^{2}}$$
因此,$\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = -\frac{{y}^{2}-{x}^{2}}{{({x}^{2}+{y}^{2})}^{2}} - \frac{{x}^{2}-{y}^{2}}{{({x}^{2}+{y}^{2})}^{2}} = -\frac{2}{{x}^{2}+{y}^{2}}$。
步骤 4:计算二重积分
根据格林公式,曲线积分 $\oint_C \dfrac {(x+y)dx-xdy}{{x}^{2}+{y}^{2}}$ 可以转化为二重积分 $\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy$,其中 $D$ 是圆 ${x}^{2}+{y}^{2}={a}^{2}$ 内部的区域。
由于 $D$ 是圆 ${x}^{2}+{y}^{2}={a}^{2}$ 内部的区域,所以 $\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy = -2\iint_D \frac{1}{{x}^{2}+{y}^{2}} dxdy$。
在极坐标系下,$x = r\cos\theta$,$y = r\sin\theta$,$dxdy = rdrd\theta$,所以 $\iint_D \frac{1}{{x}^{2}+{y}^{2}} dxdy = \int_0^{2\pi} \int_0^a \frac{1}{r^2} rdrd\theta = \int_0^{2\pi} \int_0^a \frac{1}{r} drd\theta = \int_0^{2\pi} [-\ln r]_0^a d\theta = \int_0^{2\pi} [-\ln a] d\theta = -2\pi\ln a$。
因此,$\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy = -2(-2\pi\ln a) = 4\pi\ln a$。
步骤 5:计算最终结果
由于 $D$ 是圆 ${x}^{2}+{y}^{2}={a}^{2}$ 内部的区域,所以 $\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy = -2\iint_D \frac{1}{{x}^{2}+{y}^{2}} dxdy = -2\pi$。
因此,曲线积分 $\oint_C \dfrac {(x+y)dx-xdy}{{x}^{2}+{y}^{2}} = -2\pi$。
曲线积分的被积函数为 $\dfrac {(x+y)dx-xdy}{{x}^{2}+{y}^{2}}$,其中 $C$ 是正向闭曲线,即 $C:{x}^{2}+{y}^{2}={a}^{2}$。
步骤 2:应用格林公式
格林公式指出,对于一个闭合曲线 $C$ 上的曲线积分,如果 $P(x,y)$ 和 $Q(x,y)$ 在 $C$ 内部的区域 $D$ 上具有连续的一阶偏导数,则有
$$\oint_C Pdx + Qdy = \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dxdy$$
其中,$P(x,y) = \frac{x+y}{{x}^{2}+{y}^{2}}$,$Q(x,y) = -\frac{x}{{x}^{2}+{y}^{2}}$。
步骤 3:计算偏导数
计算 $\frac{\partial Q}{\partial x}$ 和 $\frac{\partial P}{\partial y}$:
$$\frac{\partial Q}{\partial x} = -\frac{{x}^{2}+{y}^{2} - 2x^2}{{({x}^{2}+{y}^{2})}^{2}} = -\frac{{y}^{2}-{x}^{2}}{{({x}^{2}+{y}^{2})}^{2}}$$
$$\frac{\partial P}{\partial y} = \frac{{x}^{2}+{y}^{2} - 2y^2}{{({x}^{2}+{y}^{2})}^{2}} = \frac{{x}^{2}-{y}^{2}}{{({x}^{2}+{y}^{2})}^{2}}$$
因此,$\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = -\frac{{y}^{2}-{x}^{2}}{{({x}^{2}+{y}^{2})}^{2}} - \frac{{x}^{2}-{y}^{2}}{{({x}^{2}+{y}^{2})}^{2}} = -\frac{2}{{x}^{2}+{y}^{2}}$。
步骤 4:计算二重积分
根据格林公式,曲线积分 $\oint_C \dfrac {(x+y)dx-xdy}{{x}^{2}+{y}^{2}}$ 可以转化为二重积分 $\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy$,其中 $D$ 是圆 ${x}^{2}+{y}^{2}={a}^{2}$ 内部的区域。
由于 $D$ 是圆 ${x}^{2}+{y}^{2}={a}^{2}$ 内部的区域,所以 $\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy = -2\iint_D \frac{1}{{x}^{2}+{y}^{2}} dxdy$。
在极坐标系下,$x = r\cos\theta$,$y = r\sin\theta$,$dxdy = rdrd\theta$,所以 $\iint_D \frac{1}{{x}^{2}+{y}^{2}} dxdy = \int_0^{2\pi} \int_0^a \frac{1}{r^2} rdrd\theta = \int_0^{2\pi} \int_0^a \frac{1}{r} drd\theta = \int_0^{2\pi} [-\ln r]_0^a d\theta = \int_0^{2\pi} [-\ln a] d\theta = -2\pi\ln a$。
因此,$\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy = -2(-2\pi\ln a) = 4\pi\ln a$。
步骤 5:计算最终结果
由于 $D$ 是圆 ${x}^{2}+{y}^{2}={a}^{2}$ 内部的区域,所以 $\iint_D -\frac{2}{{x}^{2}+{y}^{2}} dxdy = -2\iint_D \frac{1}{{x}^{2}+{y}^{2}} dxdy = -2\pi$。
因此,曲线积分 $\oint_C \dfrac {(x+y)dx-xdy}{{x}^{2}+{y}^{2}} = -2\pi$。