题目
[题目]-|||-已知 =3(x)^3arcsin x+((x)^2+2)sqrt (1-{x)^2} ,求dy。
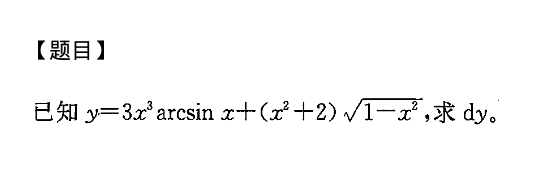
题目解答
答案

解析
考查要点:本题主要考查复合函数的求导法则,特别是乘积法则和链式法则的应用,以及微分的基本概念。
解题核心思路:
- 分解函数结构:将函数拆分为两个部分,分别求导后再相加。
- 应用乘积法则:对每个部分中的乘积项分别求导。
- 化简表达式:通过代数运算合并同类项,发现部分项相互抵消,最终得到简化结果。
破题关键点:
- 识别乘积结构:正确识别函数中的乘积项(如 $3x^3 \cdot \arcsin x$ 和 $(x^2+2) \cdot \sqrt{1-x^2}$)。
- 导数公式的应用:熟练运用 $\arcsin x$ 的导数 $\frac{1}{\sqrt{1-x^2}}$ 和 $\sqrt{1-x^2}$ 的导数 $-\frac{x}{\sqrt{1-x^2}}$。
- 代数化简技巧:通过通分合并项,发现中间项抵消的规律。
步骤1:分解函数
将 $y$ 分解为两部分:
$y = 3x^3 \arcsin x + (x^2 + 2)\sqrt{1 - x^2}$
步骤2:对第一部分求导
设 $u = 3x^3$,$v = \arcsin x$,应用乘积法则:
$\frac{d}{dx}(uv) = u'v + uv'$
- $u' = 9x^2$
- $v' = \frac{1}{\sqrt{1 - x^2}}$
因此,第一部分的导数为:
$9x^2 \arcsin x + 3x^3 \cdot \frac{1}{\sqrt{1 - x^2}}$
步骤3:对第二部分求导
设 $f = x^2 + 2$,$g = \sqrt{1 - x^2}$,应用乘积法则:
$\frac{d}{dx}(fg) = f'g + fg'$
- $f' = 2x$
- $g' = \frac{-x}{\sqrt{1 - x^2}}$
因此,第二部分的导数为:
$2x \sqrt{1 - x^2} + (x^2 + 2) \cdot \left( \frac{-x}{\sqrt{1 - x^2}} \right)$
步骤4:合并所有导数项
将两部分的导数相加:
$\begin{aligned}y' &= 9x^2 \arcsin x + \frac{3x^3}{\sqrt{1 - x^2}} + 2x \sqrt{1 - x^2} - \frac{x(x^2 + 2)}{\sqrt{1 - x^2}} \\&= 9x^2 \arcsin x + \frac{3x^3 - x(x^2 + 2)}{\sqrt{1 - x^2}} + 2x \sqrt{1 - x^2}\end{aligned}$
步骤5:化简表达式
- 处理分式项:
$3x^3 - x(x^2 + 2) = 3x^3 - x^3 - 2x = 2x^3 - 2x$ - 通分合并:
将 $2x \sqrt{1 - x^2}$ 写成 $\frac{2x(1 - x^2)}{\sqrt{1 - x^2}}$,与分式项合并:
$\frac{2x^3 - 2x + 2x(1 - x^2)}{\sqrt{1 - x^2}} = \frac{2x^3 - 2x + 2x - 2x^3}{\sqrt{1 - x^2}} = 0$ - 最终结果:
所有中间项抵消,仅剩 $y' = 9x^2 \arcsin x$。