题目
1、如果 ((x)_(0))=5, 但 ((x)_(0)-0)=f((x)_(0)+0)=4, 则limf(x)不存在。 ()
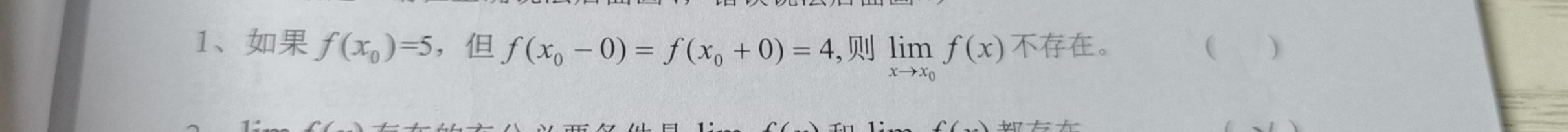
题目解答
答案

解析
考查要点:本题主要考查函数极限存在的条件,以及函数在某点处的极限与函数值的关系。
解题核心思路:
根据极限的定义,函数在某点的极限存在的充要条件是左极限和右极限都存在且相等。函数在该点的函数值不影响极限的存在性,但可能影响函数的连续性。
破题关键点:
- 题目中给出左极限 $f(x_0^-) = 4$ 和右极限 $f(x_0^+) = 4$,说明左右极限存在且相等。
- 极限的存在性与函数值无关,因此 $\lim\limits_{x \to x_0} f(x)$ 应存在且等于 $4$。
- 函数值 $f(x_0) = 5$ 与极限值不等,说明 $x_0$ 是函数的可去间断点,但极限本身存在。
关键结论:
- 极限存在条件:若 $f(x_0^-)$ 和 $f(x_0^+)$ 存在且相等,则 $\lim\limits_{x \to x_0} f(x)$ 存在且等于该值。
- 函数值不影响极限:即使 $f(x_0)$ 与极限值不同,极限仍存在。
具体分析:
- 已知 $f(x_0^-) = f(x_0^+) = 4$,说明左右极限存在且相等,因此 $\lim\limits_{x \to x_0} f(x) = 4$。
- $f(x_0) = 5$ 仅说明函数在 $x_0$ 处不连续,但不影响极限的存在性。
- 题目中“$\lim\limits_{x \to x_0} f(x)$ 不存在”的结论是错误的。