题目
函数 =tan x 在=tan x 处的变化率为____。
函数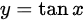 
在
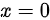处的变化率为____。
题目解答
答案
求导数或称导函数的过程就是在计算变化率；对函数 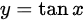求导：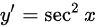
，代入x=0得:
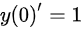，故变化率为：1.
解析
步骤 1：求导数
对函数 $y=\tan x$ 求导，得到 $y'={\sec }^{2}x$。这是因为 $\tan x$ 的导数是 ${\sec }^{2}x$，其中 $\sec x$ 是 $\cos x$ 的倒数，即 $\sec x = \frac{1}{\cos x}$。
步骤 2：代入x=0
将 $x=0$ 代入导数 $y'={\sec }^{2}x$ 中，得到 $y'(0)={\sec }^{2}0$。由于 $\sec 0 = \frac{1}{\cos 0} = \frac{1}{1} = 1$，因此 ${\sec }^{2}0 = 1^2 = 1$。
步骤 3：得出变化率
根据步骤2的计算，函数 $y=\tan x$ 在 $x=0$ 处的变化率为 $y'(0) = 1$。
对函数 $y=\tan x$ 求导，得到 $y'={\sec }^{2}x$。这是因为 $\tan x$ 的导数是 ${\sec }^{2}x$，其中 $\sec x$ 是 $\cos x$ 的倒数，即 $\sec x = \frac{1}{\cos x}$。
步骤 2：代入x=0
将 $x=0$ 代入导数 $y'={\sec }^{2}x$ 中，得到 $y'(0)={\sec }^{2}0$。由于 $\sec 0 = \frac{1}{\cos 0} = \frac{1}{1} = 1$，因此 ${\sec }^{2}0 = 1^2 = 1$。
步骤 3：得出变化率
根据步骤2的计算，函数 $y=\tan x$ 在 $x=0$ 处的变化率为 $y'(0) = 1$。