题目
6.证明恒等式: arcsin x+arccos x=dfrac (pi )(2)(-1leqslant xleqslant 1) -
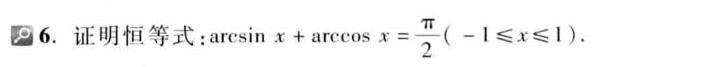
题目解答
答案

解析
步骤 1:定义函数
定义函数 $f(x)=\arcsin x+\arccos x$,其中 $x\in[-1,1]$。
步骤 2:求导
对函数 $f(x)$ 求导,得到 $f'(x)=\dfrac{1}{\sqrt{1-x^2}}-\dfrac{1}{\sqrt{1-x^2}}=0$。
步骤 3:分析导数
由于 $f'(x)=0$,说明函数 $f(x)$ 在区间 $[-1,1]$ 上是常数函数。
步骤 4:确定常数值
取 $x=0$,代入 $f(x)$,得到 $f(0)=\arcsin 0+\arccos 0=\dfrac{\pi}{2}$。
步骤 5:得出结论
因此,对于任意 $x\in[-1,1]$,有 $\arcsin x+\arccos x=\dfrac{\pi}{2}$。
定义函数 $f(x)=\arcsin x+\arccos x$,其中 $x\in[-1,1]$。
步骤 2:求导
对函数 $f(x)$ 求导,得到 $f'(x)=\dfrac{1}{\sqrt{1-x^2}}-\dfrac{1}{\sqrt{1-x^2}}=0$。
步骤 3:分析导数
由于 $f'(x)=0$,说明函数 $f(x)$ 在区间 $[-1,1]$ 上是常数函数。
步骤 4:确定常数值
取 $x=0$,代入 $f(x)$,得到 $f(0)=\arcsin 0+\arccos 0=\dfrac{\pi}{2}$。
步骤 5:得出结论
因此,对于任意 $x\in[-1,1]$,有 $\arcsin x+\arccos x=\dfrac{\pi}{2}$。