题目
证明:当时,与等价。
证明:当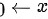 时,
时,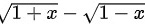 与
与 等价。
等价。
题目解答
答案
∵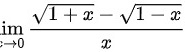
分子分母同乘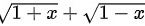 得:
得:
上式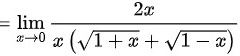
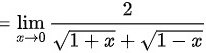
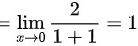
∴当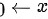 时,
时,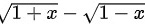 与
与 等价
等价
原题得证
解析
步骤 1:确定等价无穷小的定义
等价无穷小的定义是:当$x\rightarrow 0$时,如果$\lim _{x\rightarrow 0}\dfrac {f(x)}{g(x)}=1$,则称$f(x)$与$g(x)$是等价无穷小。
步骤 2:计算$\lim _{x\rightarrow 0}\dfrac {\sqrt {1+x}-\sqrt {1-x}}{x}$
为了计算这个极限,我们首先对分子进行有理化处理,即乘以$\sqrt {1+x}+\sqrt {1-x}$,这样可以消去根号,简化计算。
步骤 3:化简并求极限
化简后,我们得到一个可以求极限的形式,然后计算这个极限。
等价无穷小的定义是:当$x\rightarrow 0$时,如果$\lim _{x\rightarrow 0}\dfrac {f(x)}{g(x)}=1$,则称$f(x)$与$g(x)$是等价无穷小。
步骤 2:计算$\lim _{x\rightarrow 0}\dfrac {\sqrt {1+x}-\sqrt {1-x}}{x}$
为了计算这个极限,我们首先对分子进行有理化处理,即乘以$\sqrt {1+x}+\sqrt {1-x}$,这样可以消去根号,简化计算。
步骤 3:化简并求极限
化简后,我们得到一个可以求极限的形式,然后计算这个极限。