题目
11.当 k=() () 时,函数 f(x)= ) (e)^x+2,xneq 0 k, x=0 . 在 x=0 处连续.-|||-A.0 B.1 C.2 D.3
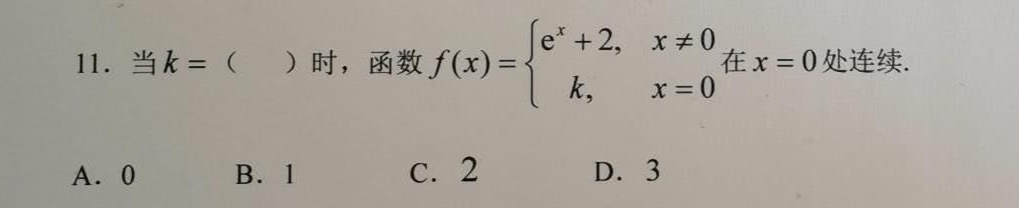
题目解答
答案

解析
步骤 1:确定函数在 x=0 处的极限
函数 $f(x)$ 在 $x=0$ 处的极限为 $\lim_{x \to 0} f(x) = \lim_{x \to 0} (e^x + 2) = e^0 + 2 = 1 + 2 = 3$。
步骤 2:确定函数在 x=0 处的值
函数 $f(x)$ 在 $x=0$ 处的值为 $f(0) = k$。
步骤 3:确定函数在 x=0 处连续的条件
函数 $f(x)$ 在 $x=0$ 处连续的条件是 $\lim_{x \to 0} f(x) = f(0)$,即 $3 = k$。
函数 $f(x)$ 在 $x=0$ 处的极限为 $\lim_{x \to 0} f(x) = \lim_{x \to 0} (e^x + 2) = e^0 + 2 = 1 + 2 = 3$。
步骤 2:确定函数在 x=0 处的值
函数 $f(x)$ 在 $x=0$ 处的值为 $f(0) = k$。
步骤 3:确定函数在 x=0 处连续的条件
函数 $f(x)$ 在 $x=0$ 处连续的条件是 $\lim_{x \to 0} f(x) = f(0)$,即 $3 = k$。