题目
设函数为(x)=(e)^(x^2+3),则(x)=(e)^(x^2+3)的值为( )。A (x)=(e)^(x^2+3) B (x)=(e)^(x^2+3)C (x)=(e)^(x^2+3) D (x)=(e)^(x^2+3)
设函数为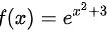 ,则
,则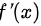 的值为( )。
的值为( )。
A 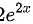
B 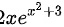
C 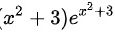
D 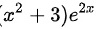
题目解答
答案
解:函数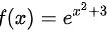 ,则
,则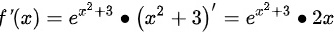 ,即
,即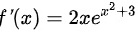 ,答案选B。
,答案选B。
解析
步骤 1:确定函数形式
函数$f(x)={e}^{{x}^{2}+3}$是一个复合函数,其中外函数是$e^u$,内函数是$u={x}^{2}+3$。
步骤 2:应用链式法则
链式法则指出,如果$y=f(u)$,$u=g(x)$,那么$y$关于$x$的导数是$y'=f'(u)\cdot g'(x)$。因此,$f'(x)={e}^{{x}^{2}+3}\cdot ({x}^{2}+3)'$。
步骤 3:计算内函数的导数
内函数$u={x}^{2}+3$的导数是$u'=2x$。
步骤 4:将内函数的导数代入
将$u'=2x$代入$f'(x)={e}^{{x}^{2}+3}\cdot ({x}^{2}+3)'$,得到$f'(x)={e}^{{x}^{2}+3}\cdot 2x$。
函数$f(x)={e}^{{x}^{2}+3}$是一个复合函数,其中外函数是$e^u$,内函数是$u={x}^{2}+3$。
步骤 2:应用链式法则
链式法则指出,如果$y=f(u)$,$u=g(x)$,那么$y$关于$x$的导数是$y'=f'(u)\cdot g'(x)$。因此,$f'(x)={e}^{{x}^{2}+3}\cdot ({x}^{2}+3)'$。
步骤 3:计算内函数的导数
内函数$u={x}^{2}+3$的导数是$u'=2x$。
步骤 4:将内函数的导数代入
将$u'=2x$代入$f'(x)={e}^{{x}^{2}+3}\cdot ({x}^{2}+3)'$,得到$f'(x)={e}^{{x}^{2}+3}\cdot 2x$。