设'(x)=arcsin ((x-1))^2 (0)=0, 求 (int )_(0)^1f(x)dx.
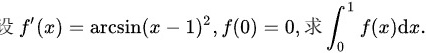
题目解答
答案


所以最终答案为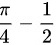
解析
考查要点:本题主要考查分部积分法的应用以及变量替换技巧,结合定积分的计算。关键在于将原积分转化为与已知导数相关联的形式,并通过变量替换简化积分表达式。
解题思路:
- 分部积分法:将原积分$\int_{0}^{1} f(x)dx$拆分为边界项和新的积分,利用已知的$f'(x)$表达式。
- 变量替换:通过替换$t = x - 1$,将积分区间转换为对称区间,简化计算。
- 对称性分析:利用奇偶函数的性质,将复杂积分转化为更易处理的形式。
- 分部积分法的二次应用:对$\int \arcsin(v) dv$进行分部积分,最终得到闭合解。
步骤1:分部积分法拆分原积分
对$\int_{0}^{1} f(x)dx$使用分部积分法:
$\int_{0}^{1} f(x)dx = \left. x f(x) \right|_{0}^{1} - \int_{0}^{1} x f'(x)dx$
其中,边界项$\left. x f(x) \right|_{0}^{1} = 1 \cdot f(1) - 0 \cdot f(0) = f(1)$,因此:
$\int_{0}^{1} f(x)dx = f(1) - \int_{0}^{1} x f'(x)dx$
步骤2:计算$f(1)$
由$f'(x) = \arcsin{(x-1)}^{2}$,积分得:
$f(1) = \int_{0}^{1} \arcsin{(x-1)}^{2} dx$
令$t = x - 1$,则积分变为:
$\int_{-1}^{0} \arcsin{t^{2}} dt = \int_{0}^{1} \arcsin{u^{2}} du \quad (u = -t)$
步骤3:处理$\int_{0}^{1} x f'(x)dx$
将积分$\int_{0}^{1} x \arcsin{(x-1)}^{2} dx$通过变量替换$t = x - 1$,得:
$\int_{-1}^{0} (t + 1) \arcsin{t^{2}} dt = \int_{-1}^{0} t \arcsin{t^{2}} dt + \int_{-1}^{0} \arcsin{t^{2}} dt$
进一步变量替换$u = -t$,得:
$\int_{0}^{1} u \arcsin{u^{2}} du + \int_{0}^{1} \arcsin{u^{2}} du = \int_{0}^{1} (u + 1) \arcsin{u^{2}} du$
步骤4:简化积分表达式
原积分变为:
$\int_{0}^{1} f(x)dx = \int_{0}^{1} \arcsin{u^{2}} du - \int_{0}^{1} u \arcsin{u^{2}} du = \int_{0}^{1} (1 - u) \arcsin{u^{2}} du$
令$v = u^{2}$,则积分进一步简化为:
$\frac{1}{2} \int_{0}^{1} \arcsin{v} dv$
步骤5:计算最终积分
对$\int \arcsin{v} dv$使用分部积分法,得:
$\int \arcsin{v} dv = v \arcsin{v} + \sqrt{1 - v^{2}} + C$
代入上下限$0$到$1$,结果为:
$\frac{1}{2} \left( \frac{\pi}{2} - 1 \right) = \frac{\pi}{4} - \frac{1}{2}$