题目
4、设曲线 y=f(x) 在[a,b]上连续,则曲线 =f(x)leqslant 0 =a, =b(alt b) 及x轴所围成-|||-图形的面积为 ()-|||-√-|||-A、 -(int )_(a)^bf(x)dx B、 (int )_(a)^b|f(x)|dx C、 (int )_(a)^bf(x)dx D、 (int )_(a)^bf(x)dx
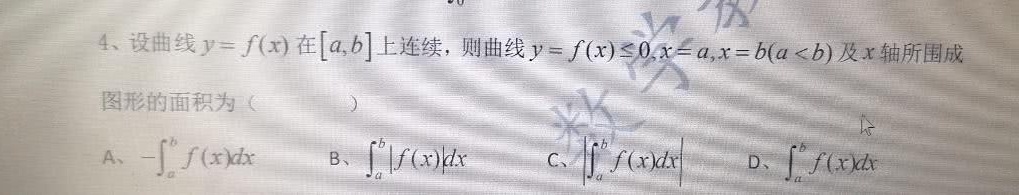
题目解答
答案

解析
步骤 1:理解题目条件
题目给出曲线 $y=f(x)$ 在区间 $[a, b]$ 上连续,且 $f(x) \leqslant 0$。这意味着函数 $f(x)$ 在区间 $[a, b]$ 上的值非正,即函数图像位于x轴下方。
步骤 2:确定面积计算方法
由于 $f(x) \leqslant 0$,直接计算积分 ${\int }_{a}^{b}f(x)dx$ 会得到一个非正的值,这与面积的定义不符。因此,需要对 $f(x)$ 取绝对值,以确保计算出的面积为正值。
步骤 3:选择正确的选项
根据上述分析,正确的面积计算方法是 ${\int }_{a}^{b}|f(x)|dx$,这将确保计算出的面积为正值。同时,由于 $f(x) \leqslant 0$,$|f(x)| = -f(x)$,因此 ${\int }_{a}^{b}|f(x)|dx = -{\int }_{a}^{b}f(x)dx$。因此,选项 A 和 B 都是正确的,而选项 C 和 D 不正确。
题目给出曲线 $y=f(x)$ 在区间 $[a, b]$ 上连续,且 $f(x) \leqslant 0$。这意味着函数 $f(x)$ 在区间 $[a, b]$ 上的值非正,即函数图像位于x轴下方。
步骤 2:确定面积计算方法
由于 $f(x) \leqslant 0$,直接计算积分 ${\int }_{a}^{b}f(x)dx$ 会得到一个非正的值,这与面积的定义不符。因此,需要对 $f(x)$ 取绝对值,以确保计算出的面积为正值。
步骤 3:选择正确的选项
根据上述分析,正确的面积计算方法是 ${\int }_{a}^{b}|f(x)|dx$,这将确保计算出的面积为正值。同时,由于 $f(x) \leqslant 0$,$|f(x)| = -f(x)$,因此 ${\int }_{a}^{b}|f(x)|dx = -{\int }_{a}^{b}f(x)dx$。因此,选项 A 和 B 都是正确的,而选项 C 和 D 不正确。