题目
讨论函数f(x)= { ,xneq 0 0, x=0 .在x=0处的连续性与可导性
讨论函数
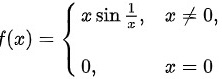
在x=0处的连续性与可导性
题目解答
答案
首先,我们来判断函数在x=0处的连续性。根据定义,我们需要计算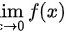 并判断其是否等于f(0)。由于当
并判断其是否等于f(0)。由于当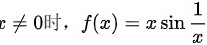 ,所以
,所以
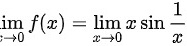
由于sin x的值域为[-1,1],所以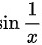 的值域也为[-1,1]。因此,对于任意
的值域也为[-1,1]。因此,对于任意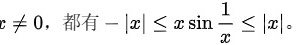 根据夹逼定理,我们有
根据夹逼定理,我们有
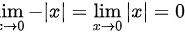
所以
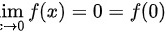
因此,函数在x=0处连续。 接下来,我们来判断函数在x=0处的可导性。根据定义,我们需要计算f'(0)并判断其是否存在。
由于x>0时,
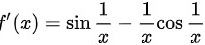
所以
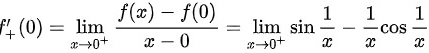
由于sin x和cos x都没有极限,所以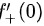 不存在。
同理,当x<0时,
不存在。
同理,当x<0时,
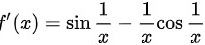
所以
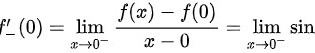
所以连续但不可导
解析
考查要点:本题主要考查分段函数在分段点处的连续性和可导性判断,需要掌握极限的计算、夹逼定理的应用,以及导数定义的理解。
解题核心思路:
- 连续性:通过计算$\lim_{x \to 0} f(x)$,结合夹逼定理判断极限是否等于$f(0)$。
- 可导性:利用导数定义,计算左右导数是否存在。若极限不存在,则函数不可导。
破题关键点:
- 连续性的关键在于利用$\sin(1/x)$有界性,结合$x \to 0$时$x$的无穷小性,通过夹逼定理求极限。
- 可导性的关键在于分析差商$\frac{f(x)-f(0)}{x}$的极限是否存在,需注意$\sin(1/x)$在$x \to 0$时的震荡特性。
连续性分析
- 计算极限:当$x \neq 0$时,$f(x) = x \sin \frac{1}{x}$。
- 由于$|\sin \frac{1}{x}| \leq 1$,故$|x \sin \frac{1}{x}| \leq |x|$。
- 根据夹逼定理,$\lim_{x \to 0} (-|x|) = \lim_{x \to 0} |x| = 0$,因此:
$\lim_{x \to 0} x \sin \frac{1}{x} = 0.$
- 比较极限与函数值:$f(0) = 0$,故$\lim_{x \to 0} f(x) = f(0)$,函数在$x=0$处连续。
可导性分析
- 导数定义:计算$f'(0)$:
$f'(0) = \lim_{x \to 0} \frac{f(x) - f(0)}{x} = \lim_{x \to 0} \frac{x \sin \frac{1}{x}}{x} = \lim_{x \to 0} \sin \frac{1}{x}.$ - 分析极限存在性:
- 当$x \to 0$时,$\frac{1}{x}$趋于无穷大,$\sin \frac{1}{x}$在$[-1, 1]$之间无限震荡,极限不存在。
- 因此,$f'(0)$不存在,函数在$x=0$处不可导。