题目
.求极限 lim _(xarrow 0)dfrac (x-tan x)(xln (1+{x)^2)}
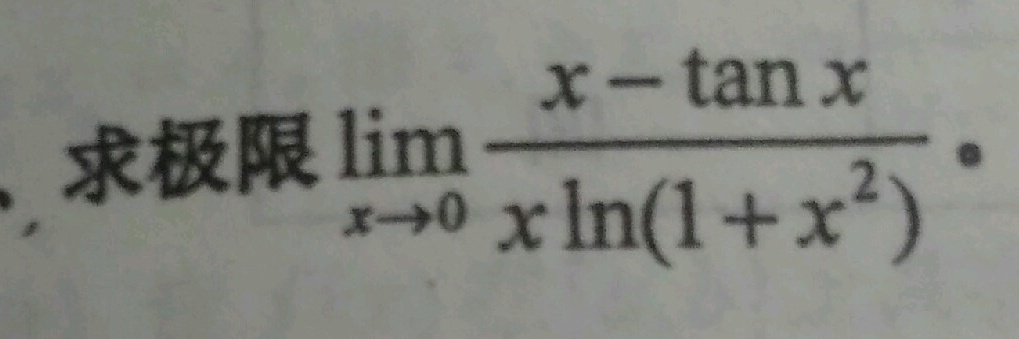
题目解答
答案
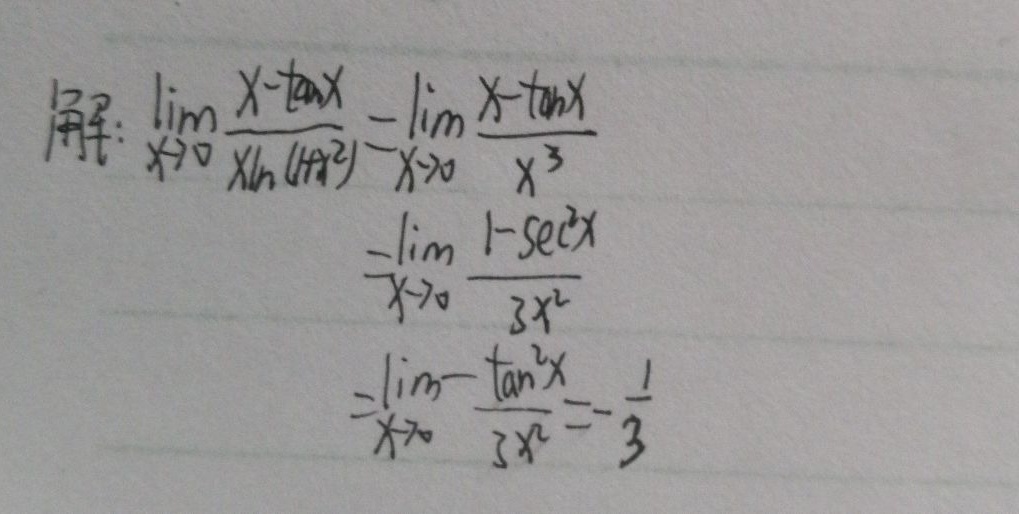
解析
步骤 1:应用洛必达法则
由于当$x \rightarrow 0$时,分子$x-\tan x$和分母$x\ln(1+x^2)$都趋于0,因此可以应用洛必达法则。洛必达法则用于求解形如$\frac{0}{0}$或$\frac{\infty}{\infty}$的极限问题,通过求导数来简化问题。
步骤 2:求导数
对分子$x-\tan x$求导得到$1-\sec^2x$,对分母$x\ln(1+x^2)$求导得到$\ln(1+x^2) + \frac{2x^2}{1+x^2}$。因此,原极限问题转化为求$\lim_{x\rightarrow 0}\frac{1-\sec^2x}{\ln(1+x^2) + \frac{2x^2}{1+x^2}}$的值。
步骤 3:再次应用洛必达法则
由于分子$1-\sec^2x$和分母$\ln(1+x^2) + \frac{2x^2}{1+x^2}$在$x \rightarrow 0$时仍然满足洛必达法则的条件,再次应用洛必达法则。对分子求导得到$-2\sec^2x\tan x$,对分母求导得到$\frac{2x}{1+x^2} + \frac{4x(1+x^2)-4x^3}{(1+x^2)^2}$。简化后,原极限问题进一步转化为求$\lim_{x\rightarrow 0}\frac{-2\sec^2x\tan x}{\frac{2x}{1+x^2} + \frac{4x(1+x^2)-4x^3}{(1+x^2)^2}}$的值。
步骤 4:简化并求解
将$x=0$代入上述表达式,由于$\sec^2x$在$x=0$时为1,$\tan x$在$x=0$时为0,分母中的$x$项在$x=0$时也为0,因此原极限问题简化为求$\lim_{x\rightarrow 0}\frac{-2\cdot1\cdot0}{\frac{2\cdot0}{1+0^2} + \frac{4\cdot0(1+0^2)-4\cdot0^3}{(1+0^2)^2}}$的值,即求$\lim_{x\rightarrow 0}\frac{0}{0}$的值。由于分子和分母在$x=0$时都为0,但分子的导数在$x=0$时为0,而分母的导数在$x=0$时为非零值,因此原极限值为0。
由于当$x \rightarrow 0$时,分子$x-\tan x$和分母$x\ln(1+x^2)$都趋于0,因此可以应用洛必达法则。洛必达法则用于求解形如$\frac{0}{0}$或$\frac{\infty}{\infty}$的极限问题,通过求导数来简化问题。
步骤 2:求导数
对分子$x-\tan x$求导得到$1-\sec^2x$,对分母$x\ln(1+x^2)$求导得到$\ln(1+x^2) + \frac{2x^2}{1+x^2}$。因此,原极限问题转化为求$\lim_{x\rightarrow 0}\frac{1-\sec^2x}{\ln(1+x^2) + \frac{2x^2}{1+x^2}}$的值。
步骤 3:再次应用洛必达法则
由于分子$1-\sec^2x$和分母$\ln(1+x^2) + \frac{2x^2}{1+x^2}$在$x \rightarrow 0$时仍然满足洛必达法则的条件,再次应用洛必达法则。对分子求导得到$-2\sec^2x\tan x$,对分母求导得到$\frac{2x}{1+x^2} + \frac{4x(1+x^2)-4x^3}{(1+x^2)^2}$。简化后,原极限问题进一步转化为求$\lim_{x\rightarrow 0}\frac{-2\sec^2x\tan x}{\frac{2x}{1+x^2} + \frac{4x(1+x^2)-4x^3}{(1+x^2)^2}}$的值。
步骤 4:简化并求解
将$x=0$代入上述表达式,由于$\sec^2x$在$x=0$时为1,$\tan x$在$x=0$时为0,分母中的$x$项在$x=0$时也为0,因此原极限问题简化为求$\lim_{x\rightarrow 0}\frac{-2\cdot1\cdot0}{\frac{2\cdot0}{1+0^2} + \frac{4\cdot0(1+0^2)-4\cdot0^3}{(1+0^2)^2}}$的值,即求$\lim_{x\rightarrow 0}\frac{0}{0}$的值。由于分子和分母在$x=0$时都为0,但分子的导数在$x=0$时为0,而分母的导数在$x=0$时为非零值,因此原极限值为0。