题目
求函数=dfrac ({2)^x}({2)^x+1}的反函数.
求函数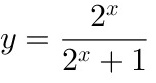 的反函数.
的反函数.
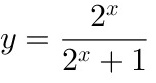 的反函数.
的反函数.题目解答
答案
解:函数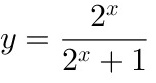 可得:
可得: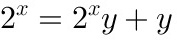 .
.
可得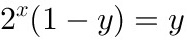 ,
,
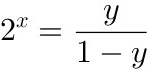 ,
,
可得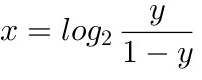 ,
,
函数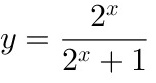 的反函数为:
的反函数为: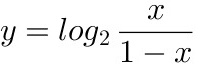 .
.
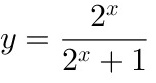 可得:
可得: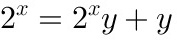 .
.可得
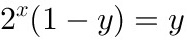 ,
,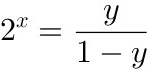 ,
,可得
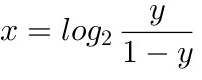 ,
,函数
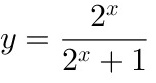 的反函数为:
的反函数为: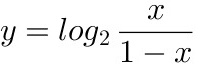 .
.解析
考查要点:本题主要考查反函数的求解方法,涉及指数方程与对数的转换,以及代数变形能力。
解题核心思路:
- 交换变量:将原函数表达式中的$x$和$y$互换,得到关于$y$的方程。
- 解方程:通过代数变形,将方程转化为以$y$表示的表达式。
- 验证定义域:根据原函数的值域确定反函数的定义域。
破题关键点:
- 分离变量:通过移项将含$2^x$的项集中,利用因式分解提取公因子。
- 对数转换:将指数形式转换为对数形式,注意对数的底数与指数的底数一致。
步骤1:交换变量并整理方程
原函数为$y = \dfrac{2^x}{2^x + 1}$,交换$x$和$y$后得到:
$x = \dfrac{2^y}{2^y + 1}$
步骤2:解关于$2^y$的方程
两边同乘分母$2^y + 1$:
$x(2^y + 1) = 2^y$
展开并整理:
$x \cdot 2^y + x = 2^y$
将含$2^y$的项移到左边:
$x \cdot 2^y - 2^y = -x$
提取公因子$2^y$:
$2^y(x - 1) = -x$
解得:
$2^y = \dfrac{-x}{x - 1} = \dfrac{x}{1 - x}$
步骤3:取对数求$y$
对等式两边取以$2$为底的对数:
$y = \log_2 \left( \dfrac{x}{1 - x} \right)$
步骤4:确定定义域
原函数$y = \dfrac{2^x}{2^x + 1}$的值域为$(0, 1)$,因此反函数的定义域为$0 < x < 1$。