题目
下列命题中正确的是A.若,则 B.若服从区间上均匀分布则C.若则D.若服从参数的指数分布,则
下列命题中正确的是
A.若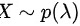 ,则
,则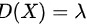
B.若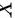 服从区间
服从区间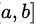 上均匀分布则
上均匀分布则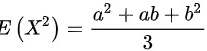
C.若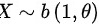 则
则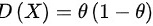
D.若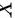 服从参数
服从参数 的指数分布,则
的指数分布,则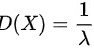
题目解答
答案
A选项: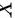 服从泊松分布,泊松分布的概率函数为
服从泊松分布,泊松分布的概率函数为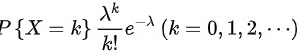 ,根据离散型随机变量分布的期望定义,泊松分布的期望和方差为:
,根据离散型随机变量分布的期望定义,泊松分布的期望和方差为: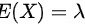 、
、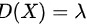 ,故A正确。
,故A正确。
B选项: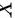 服从均匀分布,均匀分布的概率密度函数为
服从均匀分布,均匀分布的概率密度函数为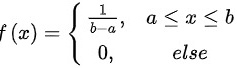 ,则
,则
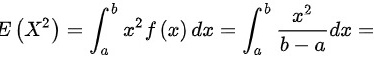
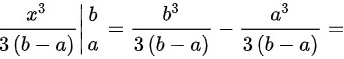
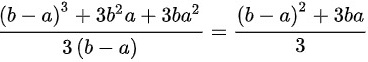
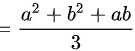 ,故B正确。
,故B正确。
C选项: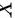 服从0-1分布,方差为
服从0-1分布,方差为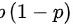 ,故C正确。
,故C正确。
D选项:若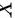 服从参数
服从参数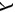 的指数分布,有
的指数分布,有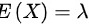 ,
,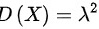 ,故D错误。
,故D错误。
答案为:ABC
解析
步骤 1:分析A选项
A选项:若$(X)d\sim X$,则$Y=(X)Q$。根据泊松分布的性质,若$X$服从泊松分布,则$Y=(X)Q$,即$Y$的期望和方差相等。因此,A选项正确。
步骤 2:分析B选项
B选项:若$X$服从区间$[a,b]$上的均匀分布,则$E(X^2)=\dfrac{{a}^{2}+ab+{b}^{2}}{3}$。根据均匀分布的性质,$E(X^2)$的计算公式为$\dfrac{{a}^{2}+ab+{b}^{2}}{3}$。因此,B选项正确。
步骤 3:分析C选项
C选项:若$X\sim b(1,\theta )$,则$D(X)=\theta (1-\theta )$。根据二项分布的性质,$D(X)=\theta (1-\theta )$。因此,C选项正确。
步骤 4:分析D选项
D选项:若$X$服从参数$\lambda$的指数分布,则$D(X)=\dfrac{1}{\lambda^2}$。根据指数分布的性质,$D(X)=\dfrac{1}{\lambda^2}$。因此,D选项错误。
A选项:若$(X)d\sim X$,则$Y=(X)Q$。根据泊松分布的性质,若$X$服从泊松分布,则$Y=(X)Q$,即$Y$的期望和方差相等。因此,A选项正确。
步骤 2:分析B选项
B选项:若$X$服从区间$[a,b]$上的均匀分布,则$E(X^2)=\dfrac{{a}^{2}+ab+{b}^{2}}{3}$。根据均匀分布的性质,$E(X^2)$的计算公式为$\dfrac{{a}^{2}+ab+{b}^{2}}{3}$。因此,B选项正确。
步骤 3:分析C选项
C选项:若$X\sim b(1,\theta )$,则$D(X)=\theta (1-\theta )$。根据二项分布的性质,$D(X)=\theta (1-\theta )$。因此,C选项正确。
步骤 4:分析D选项
D选项:若$X$服从参数$\lambda$的指数分布,则$D(X)=\dfrac{1}{\lambda^2}$。根据指数分布的性质,$D(X)=\dfrac{1}{\lambda^2}$。因此,D选项错误。