题目
6. =xarcsin dfrac (x)(2)+sqrt (4-{x)^2}
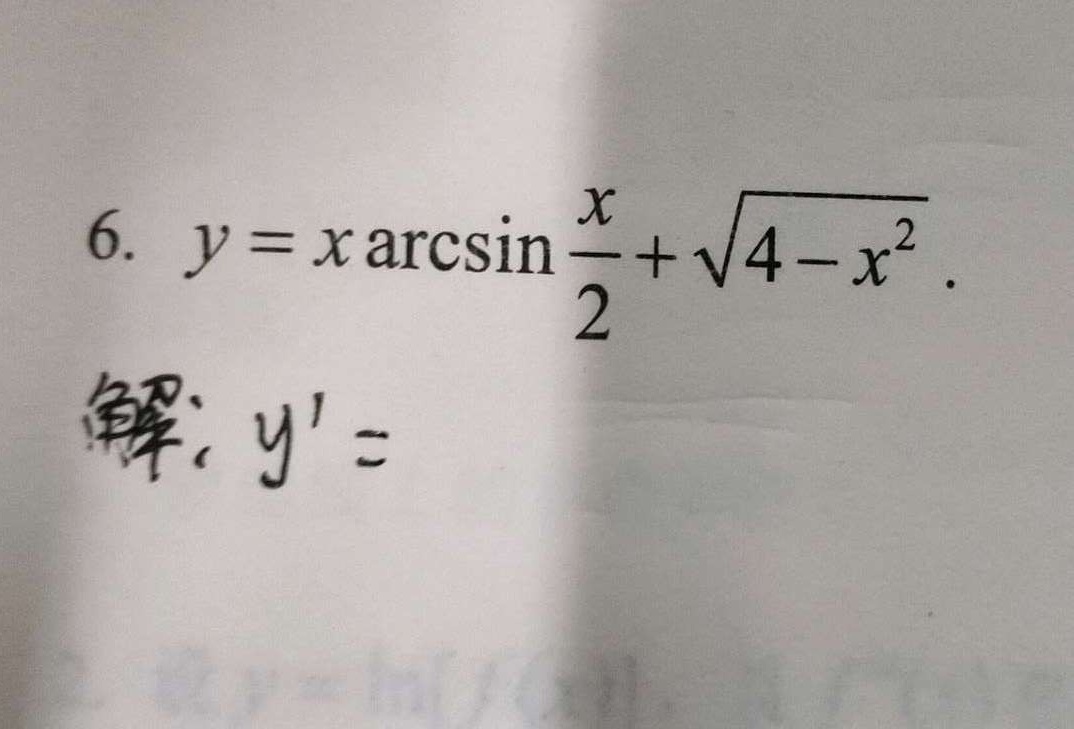
题目解答
答案

解析
考查要点:本题主要考查乘积法则和链式法则的应用,以及对反三角函数导数和根式函数导数的掌握。
解题核心思路:
- 将函数拆分为两个部分:$x \cdot \arcsin \frac{x}{2}$ 和 $\sqrt{4 - x^2}$,分别求导后相加。
- 第一部分使用乘积法则,其中$\arcsin \frac{x}{2}$的导数需用链式法则计算。
- 第二部分直接应用链式法则求导。
- 注意代数化简,确保中间步骤的符号和分母正确。
破题关键点:
- 乘积法则的正确应用,避免漏项。
- 反三角函数导数公式的准确记忆与变形。
- 代数运算中分子分母的化简,尤其是分母的平方根处理。
函数分解:
$y = x \cdot \arcsin \frac{x}{2} + \sqrt{4 - x^2}$
分步求导:
第一部分:$x \cdot \arcsin \frac{x}{2}$
- 乘积法则:
$\frac{d}{dx}[u \cdot v] = u' \cdot v + u \cdot v'$
其中 $u = x$,$v = \arcsin \frac{x}{2}$。 - 计算$u'$:
$u' = \frac{d}{dx} x = 1$ - 计算$v'$(链式法则):
$v' = \frac{d}{dx} \arcsin \frac{x}{2} = \frac{1}{\sqrt{1 - \left( \frac{x}{2} \right)^2}} \cdot \frac{1}{2} = \frac{1}{\sqrt{4 - x^2}}$ - 代入乘积法则:
$\frac{d}{dx} \left( x \cdot \arcsin \frac{x}{2} \right) = 1 \cdot \arcsin \frac{x}{2} + x \cdot \frac{1}{\sqrt{4 - x^2}}$
第二部分:$\sqrt{4 - x^2}$
- 链式法则:
$\frac{d}{dx} (4 - x^2)^{1/2} = \frac{1}{2} (4 - x^2)^{-1/2} \cdot (-2x) = -\frac{x}{\sqrt{4 - x^2}}$
合并结果
将两部分导数相加:
$\begin{aligned}y' &= \left( \arcsin \frac{x}{2} + \frac{x}{\sqrt{4 - x^2}} \right) + \left( -\frac{x}{\sqrt{4 - x^2}} \right) \\&= \arcsin \frac{x}{2}\end{aligned}$