题目
设 ,xlt 0, dfrac {x(x+1))({x)^2-1},xgeqslant 0, . 有两个第二类间断点
设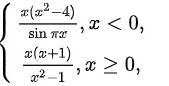
则下列正确的是（ ）。
A.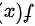
有两个第一类间断点，且都是可去间断点
B.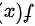有两个第一类间断点，一个是跳跃间断点，一个是可去间断点
C. 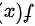只有一个第二类间断点
D. 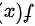有两个第二类间断点
题目解答
答案
已知函数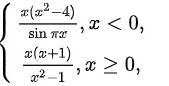
这是分段函数，需要讨论
函数的无定义点(必为间断点);
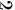分段数的分段点(可能间断也可能连续)。
(1)
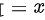是函数的无定义点，由于
,
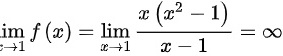故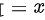为无穷间断点;
(2)
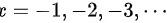也是函数的无定义点，
由于对于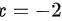
，
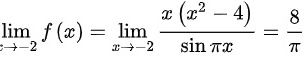
故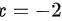为可去间断点;
对于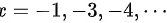
,
如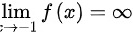
，其他点与此类似，
故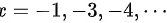为无穷间断点;
(3)
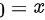是分段函数的分段点，由于
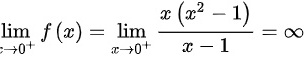
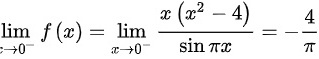
故了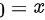为跳跃间断点。
综上所述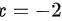，为可去间断点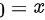，为跳跃间断点，属于第一类间断点，即有两个第一类间断点，一个是跳跃间断点，一个是可去间断点。
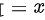为无穷间断点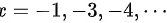，为无穷间断点，属于第二类间断点，故有无穷多个第二类间断点。
故答案为B.
解析
步骤 1：确定函数的无定义点
函数$f(x)$在$x=0$处分段，且在$x<0$时，分母为$\sin \pi x$，在$x=0$时，分母为$x^2-1$。因此，需要检查$x=0$和$x=1$处的函数值，因为$\sin \pi x$在$x=0$时为0，$x^2-1$在$x=1$时为0，这可能导致函数在这些点无定义。
步骤 2：分析$x=0$处的间断点类型
对于$x=0$，我们分别计算左右极限：
- 左极限：$\lim _{x\rightarrow 0^-}f(x)=\lim _{x\rightarrow 0^-}\dfrac {x({x}^{2}-4)}{\sin \pi x}=-\dfrac {4}{\pi }$
- 右极限：$\lim _{x\rightarrow 0^+}f(x)=\lim _{x\rightarrow 0^+}\dfrac {x({x}^{2}-1)}{x-1}=\infty$
由于左右极限不相等，$x=0$为跳跃间断点，属于第一类间断点。
步骤 3：分析$x=1$处的间断点类型
对于$x=1$，我们计算极限：
- $\lim _{x\rightarrow 1}f(x)=\lim _{x\rightarrow 1}\dfrac {x({x}^{2}-1)}{x-1}=\infty$
由于极限为无穷大，$x=1$为无穷间断点，属于第二类间断点。
步骤 4：分析$x=-2$处的间断点类型
对于$x=-2$，我们计算极限：
- $\lim _{x\rightarrow -2}f(x)=\lim _{x\rightarrow -2}\dfrac {x({x}^{2}-4)}{\sin \pi x}=\dfrac {8}{\pi }$
由于极限存在，$x=-2$为可去间断点，属于第一类间断点。
步骤 5：分析$x=-1$处的间断点类型
对于$x=-1$，我们计算极限：
- $\lim _{x\rightarrow -1}f(x)=\infty$
由于极限为无穷大，$x=-1$为无穷间断点，属于第二类间断点。
函数$f(x)$在$x=0$处分段，且在$x<0$时，分母为$\sin \pi x$，在$x=0$时，分母为$x^2-1$。因此，需要检查$x=0$和$x=1$处的函数值，因为$\sin \pi x$在$x=0$时为0，$x^2-1$在$x=1$时为0，这可能导致函数在这些点无定义。
步骤 2：分析$x=0$处的间断点类型
对于$x=0$，我们分别计算左右极限：
- 左极限：$\lim _{x\rightarrow 0^-}f(x)=\lim _{x\rightarrow 0^-}\dfrac {x({x}^{2}-4)}{\sin \pi x}=-\dfrac {4}{\pi }$
- 右极限：$\lim _{x\rightarrow 0^+}f(x)=\lim _{x\rightarrow 0^+}\dfrac {x({x}^{2}-1)}{x-1}=\infty$
由于左右极限不相等，$x=0$为跳跃间断点，属于第一类间断点。
步骤 3：分析$x=1$处的间断点类型
对于$x=1$，我们计算极限：
- $\lim _{x\rightarrow 1}f(x)=\lim _{x\rightarrow 1}\dfrac {x({x}^{2}-1)}{x-1}=\infty$
由于极限为无穷大，$x=1$为无穷间断点，属于第二类间断点。
步骤 4：分析$x=-2$处的间断点类型
对于$x=-2$，我们计算极限：
- $\lim _{x\rightarrow -2}f(x)=\lim _{x\rightarrow -2}\dfrac {x({x}^{2}-4)}{\sin \pi x}=\dfrac {8}{\pi }$
由于极限存在，$x=-2$为可去间断点，属于第一类间断点。
步骤 5：分析$x=-1$处的间断点类型
对于$x=-1$，我们计算极限：
- $\lim _{x\rightarrow -1}f(x)=\infty$
由于极限为无穷大，$x=-1$为无穷间断点，属于第二类间断点。