题目
24.函数 =xln (1-2x) 在 x=0 处的 (ngeqslant 2) 阶导数 ^(n)(0)= __ .
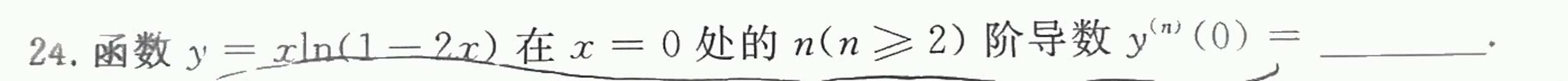
题目解答
答案
本题考查了函数的$n$阶导数,由题可得${y}^{(n)}(x)=\ln (1-2x)+{(-1)}^{n-1}\frac{n!}{{(1-2x)}^{n+1}}$$(n\in {{\mathbf{N}}^{*}})$所以${y}^{(n)}(0)=\ln (1-0)+{(-1)}^{n-1}\frac{n!}{{(1-2\times 0)}^{n+1}}={(-1)}^{n-1}\frac{n!}{{{1}^{n+1}}}={(-1)}^{n-1}n!$${(-1)}^{n-1}n!$
${(-1)}^{n-1}n!$
${(-1)}^{n-1}n!$
解析
步骤 1:求一阶导数
对函数 $y=x\ln (1-2x)$ 求一阶导数,使用乘积法则和链式法则,得到:
$y' = \ln(1-2x) + x \cdot \frac{-2}{1-2x} = \ln(1-2x) - \frac{2x}{1-2x}$
步骤 2:求二阶导数
对一阶导数 $y'$ 求导,得到二阶导数 $y''$:
$y'' = \frac{-2}{1-2x} - \frac{2(1-2x) - 2x(-2)}{(1-2x)^2} = \frac{-2}{1-2x} - \frac{2}{(1-2x)^2}$
步骤 3:求高阶导数
观察二阶导数的结构,可以发现高阶导数的通项公式。对于 $n \geqslant 2$,$y^{(n)}$ 的形式为:
$y^{(n)}(x) = \ln(1-2x) + {(-1)}^{n-1}\frac{n!}{{(1-2x)}^{n+1}}$
步骤 4:计算 $y^{(n)}(0)$
将 $x=0$ 代入 $y^{(n)}(x)$,得到:
$y^{(n)}(0) = \ln(1-0) + {(-1)}^{n-1}\frac{n!}{{(1-2\times 0)}^{n+1}} = {(-1)}^{n-1}\frac{n!}{{{1}^{n+1}}} = {(-1)}^{n-1}n!$
对函数 $y=x\ln (1-2x)$ 求一阶导数,使用乘积法则和链式法则,得到:
$y' = \ln(1-2x) + x \cdot \frac{-2}{1-2x} = \ln(1-2x) - \frac{2x}{1-2x}$
步骤 2:求二阶导数
对一阶导数 $y'$ 求导,得到二阶导数 $y''$:
$y'' = \frac{-2}{1-2x} - \frac{2(1-2x) - 2x(-2)}{(1-2x)^2} = \frac{-2}{1-2x} - \frac{2}{(1-2x)^2}$
步骤 3:求高阶导数
观察二阶导数的结构,可以发现高阶导数的通项公式。对于 $n \geqslant 2$,$y^{(n)}$ 的形式为:
$y^{(n)}(x) = \ln(1-2x) + {(-1)}^{n-1}\frac{n!}{{(1-2x)}^{n+1}}$
步骤 4:计算 $y^{(n)}(0)$
将 $x=0$ 代入 $y^{(n)}(x)$,得到:
$y^{(n)}(0) = \ln(1-0) + {(-1)}^{n-1}\frac{n!}{{(1-2\times 0)}^{n+1}} = {(-1)}^{n-1}\frac{n!}{{{1}^{n+1}}} = {(-1)}^{n-1}n!$