题目
微分方程dfrac (y)(x)+tan dfrac (y)(x)满足dfrac (y)(x)+tan dfrac (y)(x)的特解是______.
微分方程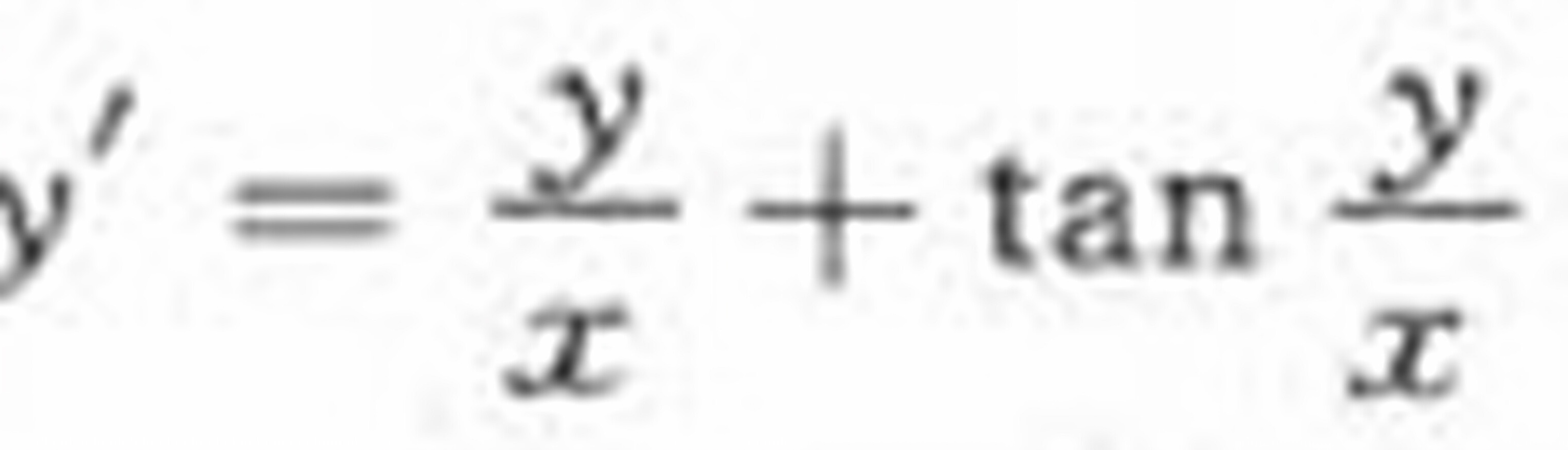 满足
满足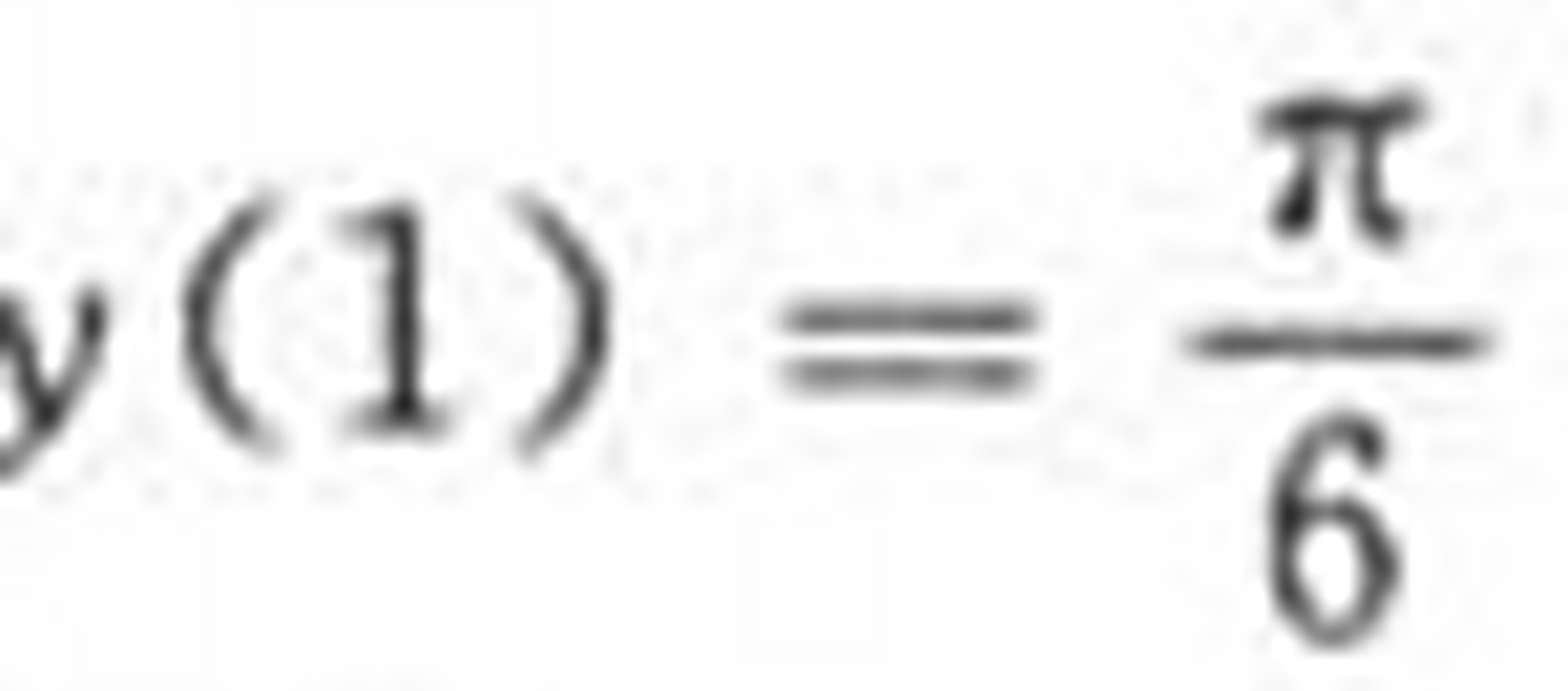 的特解是______.
的特解是______.
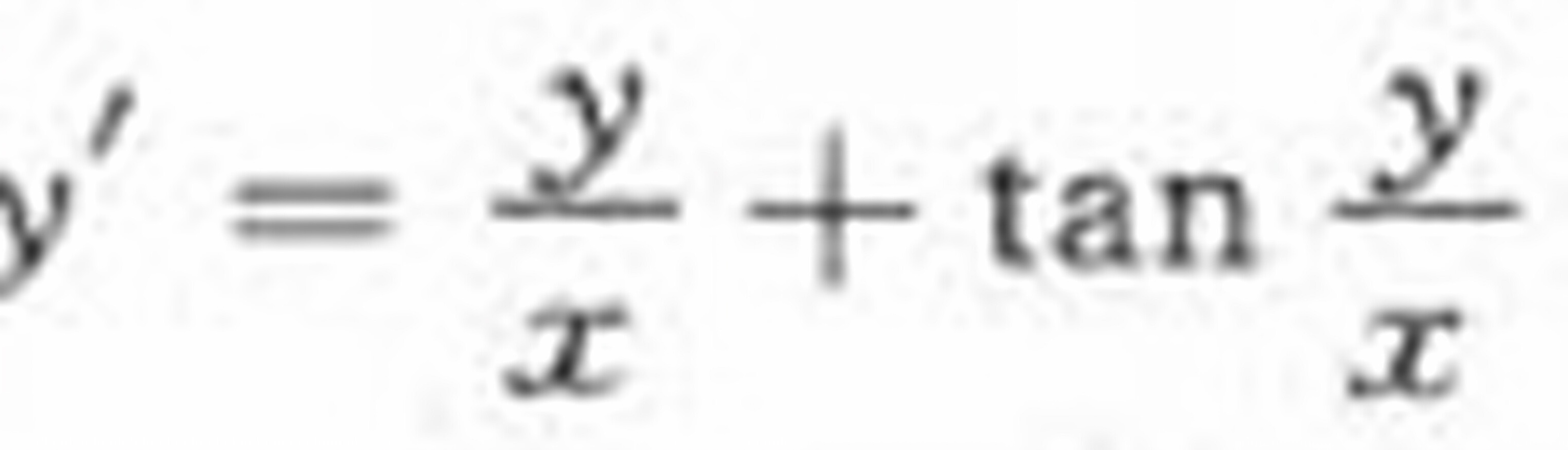 满足
满足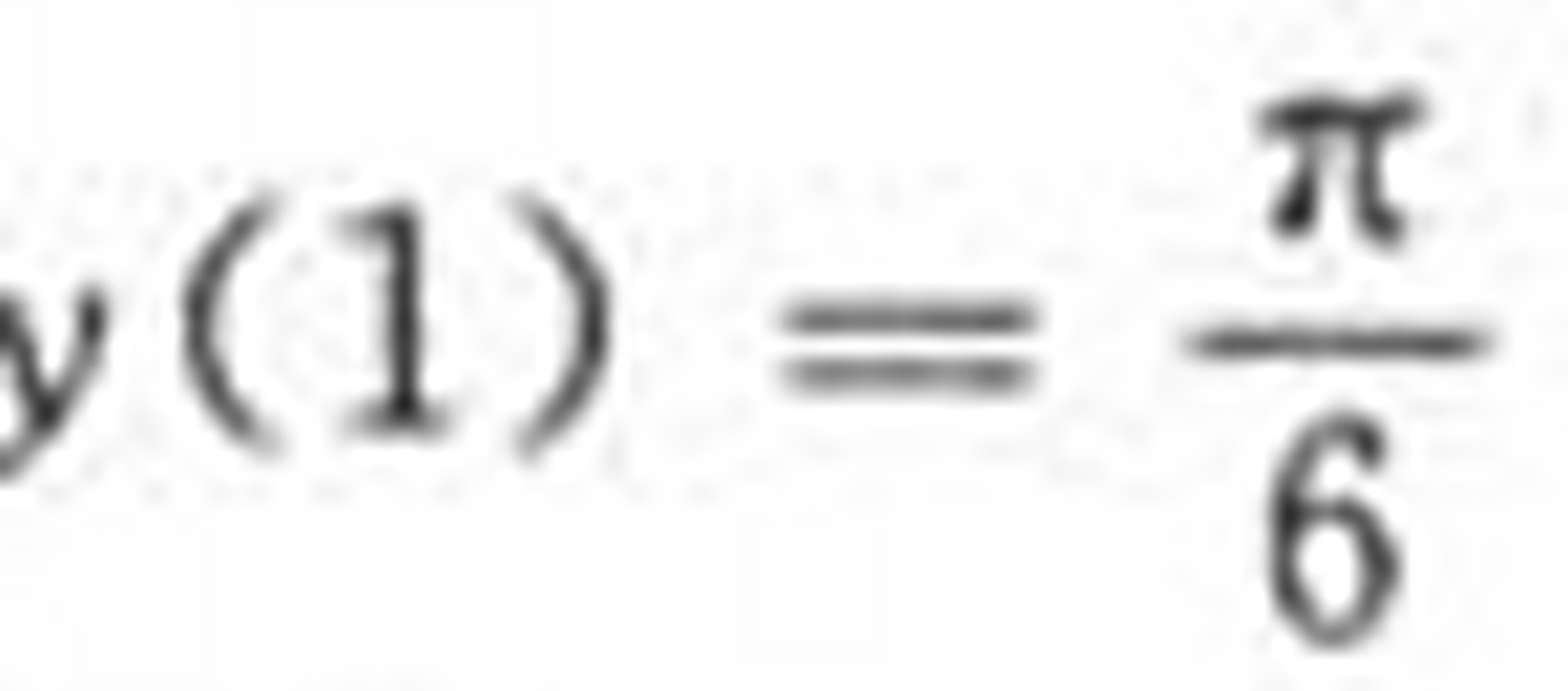 的特解是______.
的特解是______. 题目解答
答案
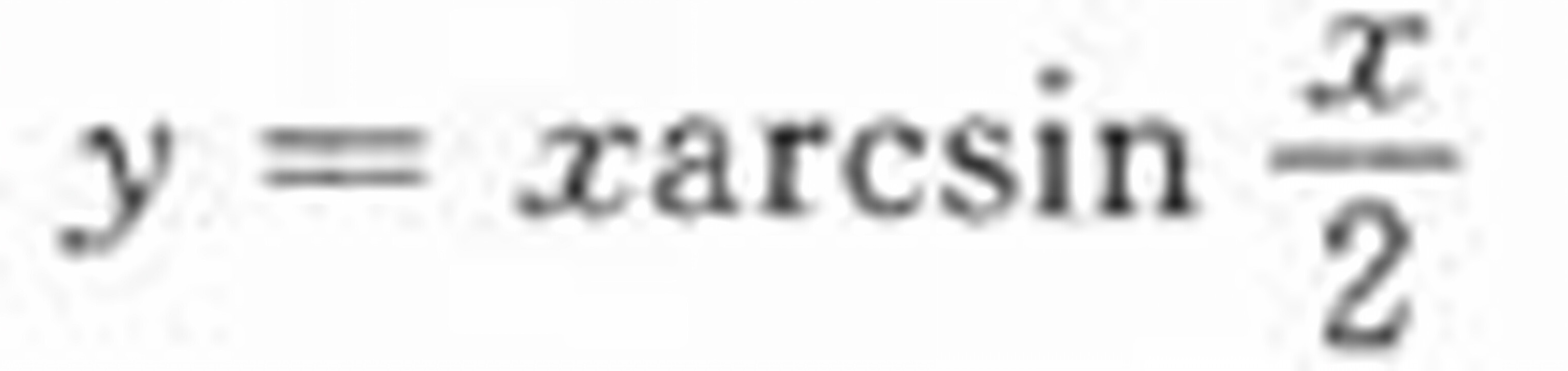
解析
步骤 1:识别方程类型
给定的微分方程是$\dfrac {y}{x}+\tan \dfrac {y}{x}$,这是一个齐次微分方程,因为方程中的每一项都是关于$\dfrac {y}{x}$的函数。
步骤 2:变量替换
设$u=\dfrac {y}{x}$,则$y=ux$,对$x$求导得到$\dfrac {dy}{dx}=u+x\dfrac {du}{dx}$。
步骤 3:代入并简化
将$y=ux$和$\dfrac {dy}{dx}=u+x\dfrac {du}{dx}$代入原方程,得到$u+x\dfrac {du}{dx}=u+\tan u$,简化后得到$x\dfrac {du}{dx}=\tan u$。
步骤 4:分离变量
分离变量得到$\dfrac {du}{\tan u}=\dfrac {dx}{x}$,即$\dfrac {\cos u}{\sin u}du=\dfrac {1}{x}dx$。
步骤 5:积分
对两边积分,得到$\int \dfrac {\cos u}{\sin u}du=\int \dfrac {1}{x}dx$,即$\ln |\sin u|=\ln |x|+C$,其中$C$是积分常数。
步骤 6:求解$u$
从$\ln |\sin u|=\ln |x|+C$得到$|\sin u|=e^C|x|$,设$e^C=k$,则$\sin u=kx$,即$\sin \dfrac {y}{x}=kx$。
步骤 7:应用初始条件
根据初始条件$y(1)=\dfrac {\pi }{6}$,代入得到$\sin \dfrac {\pi }{6}=k$,即$k=\dfrac {1}{2}$。
步骤 8:求解$y$
将$k=\dfrac {1}{2}$代入$\sin \dfrac {y}{x}=\dfrac {1}{2}x$,得到$\dfrac {y}{x}=\arcsin \dfrac {x}{2}$,即$y=x\arcsin \dfrac {x}{2}$。
给定的微分方程是$\dfrac {y}{x}+\tan \dfrac {y}{x}$,这是一个齐次微分方程,因为方程中的每一项都是关于$\dfrac {y}{x}$的函数。
步骤 2:变量替换
设$u=\dfrac {y}{x}$,则$y=ux$,对$x$求导得到$\dfrac {dy}{dx}=u+x\dfrac {du}{dx}$。
步骤 3:代入并简化
将$y=ux$和$\dfrac {dy}{dx}=u+x\dfrac {du}{dx}$代入原方程,得到$u+x\dfrac {du}{dx}=u+\tan u$,简化后得到$x\dfrac {du}{dx}=\tan u$。
步骤 4:分离变量
分离变量得到$\dfrac {du}{\tan u}=\dfrac {dx}{x}$,即$\dfrac {\cos u}{\sin u}du=\dfrac {1}{x}dx$。
步骤 5:积分
对两边积分,得到$\int \dfrac {\cos u}{\sin u}du=\int \dfrac {1}{x}dx$,即$\ln |\sin u|=\ln |x|+C$,其中$C$是积分常数。
步骤 6:求解$u$
从$\ln |\sin u|=\ln |x|+C$得到$|\sin u|=e^C|x|$,设$e^C=k$,则$\sin u=kx$,即$\sin \dfrac {y}{x}=kx$。
步骤 7:应用初始条件
根据初始条件$y(1)=\dfrac {\pi }{6}$,代入得到$\sin \dfrac {\pi }{6}=k$,即$k=\dfrac {1}{2}$。
步骤 8:求解$y$
将$k=\dfrac {1}{2}$代入$\sin \dfrac {y}{x}=\dfrac {1}{2}x$,得到$\dfrac {y}{x}=\arcsin \dfrac {x}{2}$,即$y=x\arcsin \dfrac {x}{2}$。