题目
已知 =ln (cos 4x),则 =ln (cos 4x)
已知 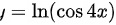 ,则
,则 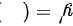
题目解答
答案
由题意,已知
函数 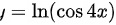
令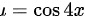
则,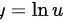
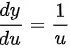
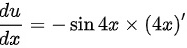
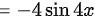
将其代入复合函数求导法则计算,得
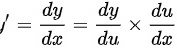
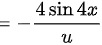
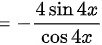
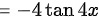
解析
步骤 1:定义函数
已知函数 $y=\ln (\cos 4x)$,这是一个复合函数,其中外函数为 $y=\ln u$,内函数为 $u=\cos 4x$。
步骤 2:求内函数的导数
对内函数 $u=\cos 4x$ 求导,得到 $\dfrac {du}{dx}=-\sin 4x \times (4x)'=-4\sin 4x$。
步骤 3:应用复合函数求导法则
根据复合函数求导法则,$y'=\dfrac {dy}{dx}=\dfrac {dy}{du}\times \dfrac {du}{dx}$,其中 $\dfrac {dy}{du}=\dfrac {1}{u}$,代入 $\dfrac {du}{dx}=-4\sin 4x$,得到 $y'=\dfrac {1}{\cos 4x} \times (-4\sin 4x)=-4\tan 4x$。
已知函数 $y=\ln (\cos 4x)$,这是一个复合函数,其中外函数为 $y=\ln u$,内函数为 $u=\cos 4x$。
步骤 2:求内函数的导数
对内函数 $u=\cos 4x$ 求导,得到 $\dfrac {du}{dx}=-\sin 4x \times (4x)'=-4\sin 4x$。
步骤 3:应用复合函数求导法则
根据复合函数求导法则,$y'=\dfrac {dy}{dx}=\dfrac {dy}{du}\times \dfrac {du}{dx}$,其中 $\dfrac {dy}{du}=\dfrac {1}{u}$,代入 $\dfrac {du}{dx}=-4\sin 4x$,得到 $y'=\dfrac {1}{\cos 4x} \times (-4\sin 4x)=-4\tan 4x$。