题目
8 若 lim _(xarrow 0)(dfrac (sin 3{x)^2+(x)^2f(x)}({x)^6})=0 则 lim _(xarrow 0)dfrac (3+f(x))({x)^4} 为-|||-(A)0. (B)3. (C) 9/2. (D) times ,
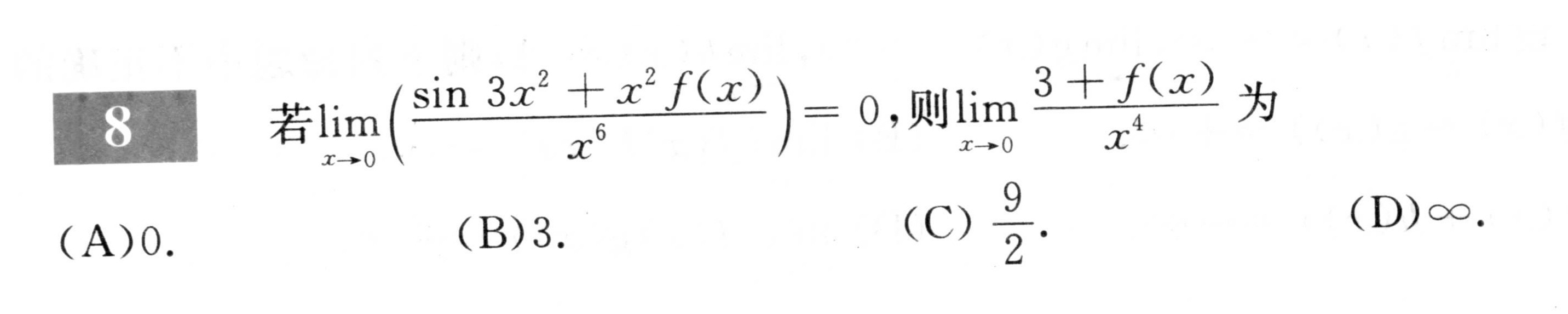
题目解答
答案

解析
步骤 1:分析给定的极限条件
给定条件为 $\lim _{x\rightarrow 0}(\sin 3x^2 + x^2f(x))=0$。这意味着当 $x$ 趋近于 0 时,$\sin 3x^2 + x^2f(x)$ 的值趋近于 0。
步骤 2:利用泰勒公式展开 $\sin 3x^2$
根据泰勒公式,$\sin t = t - \frac{1}{3!}t^3 + o(t^3)$,当 $t \rightarrow 0$。令 $t = 3x^2$,则有 $\sin 3x^2 = 3x^2 - \frac{1}{6}(3x^2)^3 + o(x^6)$。简化后得到 $\sin 3x^2 = 3x^2 - \frac{9}{2}x^6 + o(x^6)$。
步骤 3:将 $\sin 3x^2$ 的展开式代入给定条件
将 $\sin 3x^2 = 3x^2 - \frac{9}{2}x^6 + o(x^6)$ 代入 $\lim _{x\rightarrow 0}(\sin 3x^2 + x^2f(x))=0$,得到 $\lim _{x\rightarrow 0}(3x^2 - \frac{9}{2}x^6 + x^2f(x) + o(x^6))=0$。由于 $x^2f(x)$ 和 $o(x^6)$ 在 $x \rightarrow 0$ 时都趋近于 0,因此可以得到 $\lim _{x\rightarrow 0}(3x^2 - \frac{9}{2}x^6 + x^2f(x))=0$。
步骤 4:求解 $\lim _{x\rightarrow 0}\dfrac {3+f(x)}{{x}^{4}}$
根据步骤 3 的结果,可以得到 $\lim _{x\rightarrow 0}\dfrac {3x^2 - \frac{9}{2}x^6 + x^2f(x)}{x^4} = 0$。将分子除以 $x^2$,得到 $\lim _{x\rightarrow 0}\dfrac {3 - \frac{9}{2}x^4 + f(x)}{x^2} = 0$。进一步得到 $\lim _{x\rightarrow 0}\dfrac {3 + f(x)}{x^2} = \frac{9}{2}$。因此,$\lim _{x\rightarrow 0}\dfrac {3 + f(x)}{x^4} = \frac{9}{2}$。
给定条件为 $\lim _{x\rightarrow 0}(\sin 3x^2 + x^2f(x))=0$。这意味着当 $x$ 趋近于 0 时,$\sin 3x^2 + x^2f(x)$ 的值趋近于 0。
步骤 2:利用泰勒公式展开 $\sin 3x^2$
根据泰勒公式,$\sin t = t - \frac{1}{3!}t^3 + o(t^3)$,当 $t \rightarrow 0$。令 $t = 3x^2$,则有 $\sin 3x^2 = 3x^2 - \frac{1}{6}(3x^2)^3 + o(x^6)$。简化后得到 $\sin 3x^2 = 3x^2 - \frac{9}{2}x^6 + o(x^6)$。
步骤 3:将 $\sin 3x^2$ 的展开式代入给定条件
将 $\sin 3x^2 = 3x^2 - \frac{9}{2}x^6 + o(x^6)$ 代入 $\lim _{x\rightarrow 0}(\sin 3x^2 + x^2f(x))=0$,得到 $\lim _{x\rightarrow 0}(3x^2 - \frac{9}{2}x^6 + x^2f(x) + o(x^6))=0$。由于 $x^2f(x)$ 和 $o(x^6)$ 在 $x \rightarrow 0$ 时都趋近于 0,因此可以得到 $\lim _{x\rightarrow 0}(3x^2 - \frac{9}{2}x^6 + x^2f(x))=0$。
步骤 4:求解 $\lim _{x\rightarrow 0}\dfrac {3+f(x)}{{x}^{4}}$
根据步骤 3 的结果,可以得到 $\lim _{x\rightarrow 0}\dfrac {3x^2 - \frac{9}{2}x^6 + x^2f(x)}{x^4} = 0$。将分子除以 $x^2$,得到 $\lim _{x\rightarrow 0}\dfrac {3 - \frac{9}{2}x^4 + f(x)}{x^2} = 0$。进一步得到 $\lim _{x\rightarrow 0}\dfrac {3 + f(x)}{x^2} = \frac{9}{2}$。因此,$\lim _{x\rightarrow 0}\dfrac {3 + f(x)}{x^4} = \frac{9}{2}$。