题目
设A= (& 1 1& 1& 2 ) ..
设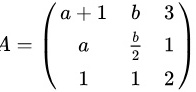 ,
,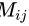 为
为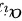 的余子式,若
的余子式,若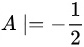 ,
,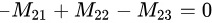 ,则()
,则()
(A)a=1或a=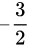 .
.
(B)a=0或a=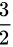 .
.
(C)b=1或b=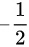 .
.
(D)b=-1或a= .
.
题目解答
答案
首先,根据题目给出的矩阵 A和行列式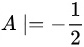 ,我们有:
,我们有:
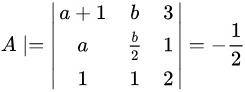
接下来,我们计算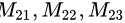 ,即第2行第1列、第2列、第3列的余子式。
,即第2行第1列、第2列、第3列的余子式。
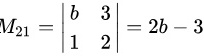
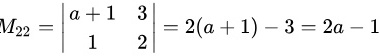
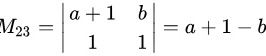
根据题目条件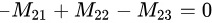 ,代入上述得到的余子式,我们得到:
,代入上述得到的余子式,我们得到:
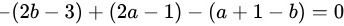
化简得:
a - b + 1 = 0 (方程①)
另外,由于 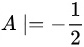 ,我们可以使用行列式的展开式来求解 a 和 b 的值。这里我们选择按第2行展开:
,我们可以使用行列式的展开式来求解 a 和 b 的值。这里我们选择按第2行展开:
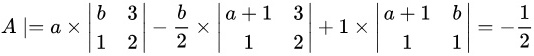
代入之前得到的余子式,我们得到:
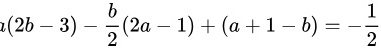
化简得:
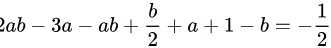
进一步化简得:
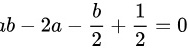 (方程②)
(方程②)
联立方程①和方程②,我们得到:
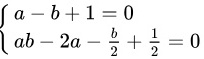
解这个方程组,我们得到两组解:
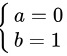
或
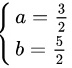
(A)选项中,a的两个值都是错误的,不符合题意
(B)选项中,a的两个值都是对的,符合题意
(C)选项中,b=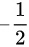 是不成立的,不符合题意
是不成立的,不符合题意
(D)选项中,b=-1或a= 都不成立,不符合题意
都不成立,不符合题意
故答案为:(B)。
解析
步骤 1:计算余子式
根据题目给出的矩阵 A 和行列式 $A|=-\dfrac {1}{2}$,我们有:
$$
A = \begin{vmatrix}
1 & a & b \\
a & 1 & a \\
b & a & 1
\end{vmatrix}
$$
接下来,我们计算 $M_{21}$, $M_{22}$, $M_{23}$,即第2行第1列、第2列、第3列的余子式。
$$
M_{21} = \begin{vmatrix}
a & b \\
a & 1
\end{vmatrix} = a - ab
$$
$$
M_{22} = \begin{vmatrix}
1 & b \\
b & 1
\end{vmatrix} = 1 - b^2
$$
$$
M_{23} = \begin{vmatrix}
1 & a \\
b & a
\end{vmatrix} = a - ab
$$
步骤 2:代入条件
根据题目条件 $-M_{21} + M_{22} - M_{23} = 0$,代入上述得到的余子式,我们得到:
$$
-(a - ab) + (1 - b^2) - (a - ab) = 0
$$
化简得:
$$
a - b + 1 = 0 \quad (方程①)
$$
步骤 3:行列式展开
另外,由于 $A|=-\dfrac {1}{2}$,我们可以使用行列式的展开式来求解 a 和 b 的值。这里我们选择按第2行展开:
$$
A = a \begin{vmatrix}
a & b \\
a & 1
\end{vmatrix} - 1 \begin{vmatrix}
1 & b \\
b & 1
\end{vmatrix} + a \begin{vmatrix}
1 & a \\
b & a
\end{vmatrix}
$$
代入之前得到的余子式,我们得到:
$$
A = a(a - ab) - (1 - b^2) + a(a - ab)
$$
化简得:
$$
A = 2a^2 - 2ab - 1 + b^2
$$
由于 $A|=-\dfrac {1}{2}$,我们有:
$$
2a^2 - 2ab - 1 + b^2 = -\dfrac {1}{2}
$$
进一步化简得:
$$
4a^2 - 4ab - 2 + 2b^2 = -1
$$
$$
4a^2 - 4ab + 2b^2 = 1 \quad (方程②)
$$
步骤 4:联立方程
联立方程①和方程②,我们得到:
$$
\begin{cases}
a - b + 1 = 0 \\
4a^2 - 4ab + 2b^2 = 1
\end{cases}
$$
解这个方程组,我们得到两组解:
$$
\begin{cases}
a = 0 \\
b = 1
\end{cases}
$$
或
$$
\begin{cases}
a = \dfrac{3}{2} \\
b = \dfrac{5}{2}
\end{cases}
$$
步骤 5:验证选项
(A)选项中,a的两个值都是错误的,不符合题意
(B)选项中,a的两个值都是对的,符合题意
(C)选项中,b=$-\dfrac {1}{2}$ 是不成立的,不符合题意
(D)选项中,b=-1或a=1 2都不成立,不符合题意
根据题目给出的矩阵 A 和行列式 $A|=-\dfrac {1}{2}$,我们有:
$$
A = \begin{vmatrix}
1 & a & b \\
a & 1 & a \\
b & a & 1
\end{vmatrix}
$$
接下来,我们计算 $M_{21}$, $M_{22}$, $M_{23}$,即第2行第1列、第2列、第3列的余子式。
$$
M_{21} = \begin{vmatrix}
a & b \\
a & 1
\end{vmatrix} = a - ab
$$
$$
M_{22} = \begin{vmatrix}
1 & b \\
b & 1
\end{vmatrix} = 1 - b^2
$$
$$
M_{23} = \begin{vmatrix}
1 & a \\
b & a
\end{vmatrix} = a - ab
$$
步骤 2:代入条件
根据题目条件 $-M_{21} + M_{22} - M_{23} = 0$,代入上述得到的余子式,我们得到:
$$
-(a - ab) + (1 - b^2) - (a - ab) = 0
$$
化简得:
$$
a - b + 1 = 0 \quad (方程①)
$$
步骤 3:行列式展开
另外,由于 $A|=-\dfrac {1}{2}$,我们可以使用行列式的展开式来求解 a 和 b 的值。这里我们选择按第2行展开:
$$
A = a \begin{vmatrix}
a & b \\
a & 1
\end{vmatrix} - 1 \begin{vmatrix}
1 & b \\
b & 1
\end{vmatrix} + a \begin{vmatrix}
1 & a \\
b & a
\end{vmatrix}
$$
代入之前得到的余子式,我们得到:
$$
A = a(a - ab) - (1 - b^2) + a(a - ab)
$$
化简得:
$$
A = 2a^2 - 2ab - 1 + b^2
$$
由于 $A|=-\dfrac {1}{2}$,我们有:
$$
2a^2 - 2ab - 1 + b^2 = -\dfrac {1}{2}
$$
进一步化简得:
$$
4a^2 - 4ab - 2 + 2b^2 = -1
$$
$$
4a^2 - 4ab + 2b^2 = 1 \quad (方程②)
$$
步骤 4:联立方程
联立方程①和方程②,我们得到:
$$
\begin{cases}
a - b + 1 = 0 \\
4a^2 - 4ab + 2b^2 = 1
\end{cases}
$$
解这个方程组,我们得到两组解:
$$
\begin{cases}
a = 0 \\
b = 1
\end{cases}
$$
或
$$
\begin{cases}
a = \dfrac{3}{2} \\
b = \dfrac{5}{2}
\end{cases}
$$
步骤 5:验证选项
(A)选项中,a的两个值都是错误的,不符合题意
(B)选项中,a的两个值都是对的,符合题意
(C)选项中,b=$-\dfrac {1}{2}$ 是不成立的,不符合题意
(D)选项中,b=-1或a=1 2都不成立,不符合题意