题目
[例1.25] 求极限 lim _(xarrow infty )((sin dfrac {1)(x)+cos dfrac (1)(x))}^x.
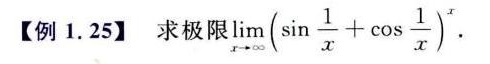
题目解答
答案

解析
步骤 1:确定极限类型
给定的极限 $\lim _{x\rightarrow \infty }{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}$ 是一个 $1^\infty$ 型未定式,因为当 $x \rightarrow \infty$ 时,$\sin \dfrac {1}{x}+\cos \dfrac {1}{x} \rightarrow 1$,而指数 $x \rightarrow \infty$。
步骤 2:转换为指数函数形式
为了处理这种类型的极限,我们可以将其转换为指数函数的形式。设 $y = {(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}$,则 $\ln y = x \ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})$。因此,原极限可以写为 $\lim _{x\rightarrow \infty } \ln y = \lim _{x\rightarrow \infty } x \ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})$。
步骤 3:应用洛必达法则
由于 $\lim _{x\rightarrow \infty } x \ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})$ 是一个 $\infty \cdot 0$ 型未定式,我们可以将其转换为 $\lim _{x\rightarrow \infty } \dfrac {\ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}{\dfrac {1}{x}}$,这是一个 $\dfrac {0}{0}$ 型未定式,可以应用洛必达法则。应用洛必达法则,我们得到:
$$
\lim _{x\rightarrow \infty } \dfrac {\ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}{\dfrac {1}{x}} = \lim _{x\rightarrow \infty } \dfrac {\dfrac {1}{\sin \dfrac {1}{x}+\cos \dfrac {1}{x}} \cdot (-\dfrac {1}{x^2} \cos \dfrac {1}{x} + \dfrac {1}{x^2} \sin \dfrac {1}{x})}{-\dfrac {1}{x^2}} = \lim _{x\rightarrow \infty } \dfrac {\sin \dfrac {1}{x} - \cos \dfrac {1}{x}}{\sin \dfrac {1}{x} + \cos \dfrac {1}{x}} = 1
$$
因此,$\lim _{x\rightarrow \infty } \ln y = 1$,所以 $\lim _{x\rightarrow \infty } y = e^1 = e$。
给定的极限 $\lim _{x\rightarrow \infty }{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}$ 是一个 $1^\infty$ 型未定式,因为当 $x \rightarrow \infty$ 时,$\sin \dfrac {1}{x}+\cos \dfrac {1}{x} \rightarrow 1$,而指数 $x \rightarrow \infty$。
步骤 2:转换为指数函数形式
为了处理这种类型的极限,我们可以将其转换为指数函数的形式。设 $y = {(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}$,则 $\ln y = x \ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})$。因此,原极限可以写为 $\lim _{x\rightarrow \infty } \ln y = \lim _{x\rightarrow \infty } x \ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})$。
步骤 3:应用洛必达法则
由于 $\lim _{x\rightarrow \infty } x \ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})$ 是一个 $\infty \cdot 0$ 型未定式,我们可以将其转换为 $\lim _{x\rightarrow \infty } \dfrac {\ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}{\dfrac {1}{x}}$,这是一个 $\dfrac {0}{0}$ 型未定式,可以应用洛必达法则。应用洛必达法则,我们得到:
$$
\lim _{x\rightarrow \infty } \dfrac {\ln (\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}{\dfrac {1}{x}} = \lim _{x\rightarrow \infty } \dfrac {\dfrac {1}{\sin \dfrac {1}{x}+\cos \dfrac {1}{x}} \cdot (-\dfrac {1}{x^2} \cos \dfrac {1}{x} + \dfrac {1}{x^2} \sin \dfrac {1}{x})}{-\dfrac {1}{x^2}} = \lim _{x\rightarrow \infty } \dfrac {\sin \dfrac {1}{x} - \cos \dfrac {1}{x}}{\sin \dfrac {1}{x} + \cos \dfrac {1}{x}} = 1
$$
因此,$\lim _{x\rightarrow \infty } \ln y = 1$,所以 $\lim _{x\rightarrow \infty } y = e^1 = e$。