设随机变量的概率密度函数为,记,则( )A. B. C. D.
设随机变量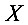 的概率密度函数为
的概率密度函数为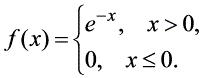 ,记
,记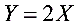 ,则
,则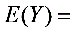 ( )
( )
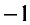
B.
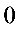
C.
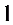
D.
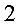
题目解答
答案
D
解析
考查要点:本题主要考查概率密度函数的变量变换,涉及指数分布的性质及线性变换后的密度函数推导。
解题核心思路:
当随机变量$Y$与原变量$X$满足线性关系$Y = aX + b$时,可通过累积分布函数法或概率密度函数变换法求解$Y$的密度函数。本题中$Y = 2X$,需通过变量代换和导数运算得到$Y$的密度函数。
破题关键点:
- 确定原变量$X$的密度函数形式(指数分布);
- 建立$Y$的累积分布函数与$X$的关系;
- 对累积分布函数求导得到$Y$的密度函数,注意链式法则的应用。
步骤1:写出原变量$X$的累积分布函数
$X$的概率密度函数为:
$f_X(x) =
\begin{cases} e^{-x}, & x > 0, \\0, & x \leq 0.\end{cases}$
其累积分布函数为:
$F_X(x) =
\begin{cases} 1 - e^{-x}, & x > 0, \\0, & x \leq 0.\end{cases}$
步骤2:建立$Y$的累积分布函数
由$Y = 2X$,当$y > 0$时:
$F_Y(y) = P(Y \leq y) = P(2X \leq y) = P\left(X \leq \frac{y}{2}\right) = F_X\left(\frac{y}{2}\right).$
当$y \leq 0$时,$F_Y(y) = 0$。
步骤3:对累积分布函数求导
对$F_Y(y)$求导得$Y$的密度函数:
$f_Y(y) = \frac{d}{dy} F_Y(y) = \frac{d}{dy} F_X\left(\frac{y}{2}\right) = f_X\left(\frac{y}{2}\right) \cdot \frac{1}{2}.$
代入$f_X(x) = e^{-x}$得:
$f_Y(y) =
\begin{cases} \frac{1}{2} e^{-y/2}, & y > 0, \\0, & y \leq 0.\end{cases}$
结论:$Y$服从参数为$\lambda = \frac{1}{2}$的指数分布,其密度函数为$\frac{1}{2} e^{-y/2}$(对应选项D)。