题目
28、 dfrac (d)(dx)(int )_(1)^2arctan xdx= __-|||-_
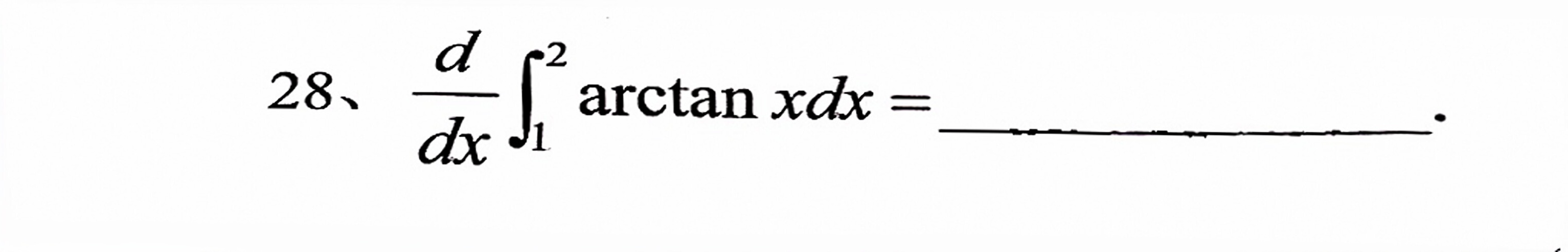
题目解答
答案

解析
步骤 1:理解问题
题目要求我们计算函数 $\dfrac {d}{dx}{\int }_{1}^{2}\arctan xdx$ 的值。这里,我们注意到积分的上下限是常数,这意味着积分的结果是一个常数,而不是一个关于 $x$ 的函数。
步骤 2:计算积分
积分 ${\int }_{1}^{2}\arctan xdx$ 是一个关于 $x$ 的定积分,其结果是一个常数。由于积分的上下限是常数,积分的结果不会随 $x$ 的变化而变化。
步骤 3:求导
由于积分的结果是一个常数,对这个常数求导的结果是 0。因此,$\dfrac {d}{dx}{\int }_{1}^{2}\arctan xdx=0$。
题目要求我们计算函数 $\dfrac {d}{dx}{\int }_{1}^{2}\arctan xdx$ 的值。这里,我们注意到积分的上下限是常数,这意味着积分的结果是一个常数,而不是一个关于 $x$ 的函数。
步骤 2:计算积分
积分 ${\int }_{1}^{2}\arctan xdx$ 是一个关于 $x$ 的定积分,其结果是一个常数。由于积分的上下限是常数,积分的结果不会随 $x$ 的变化而变化。
步骤 3:求导
由于积分的结果是一个常数,对这个常数求导的结果是 0。因此,$\dfrac {d}{dx}{\int }_{1}^{2}\arctan xdx=0$。