(此题总分值6分)求微分方程dfrac (dy)(dx)=dfrac (y-sqrt {{x)^2+(y)^2}}(x)的通解.
(此题总分值6分)
求微分方程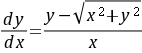 的通解.
的通解.
题目解答
答案
[解析]令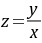 ,那么
,那么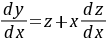 .
.
当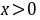 时,原方程化为
时,原方程化为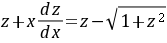 ,即
,即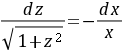 ,其通解为
,其通解为
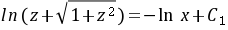 或
或 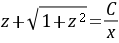 .
.
代回原变量,得通解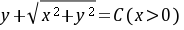 .
.
当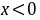 时,原方程的解与
时,原方程的解与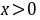 时一样,理由如下:
时一样,理由如下:
令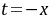 ,于是
,于是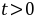 ,而且
,而且
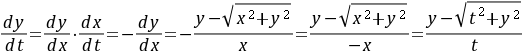 .
.
从而有通解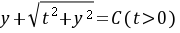 ,即
,即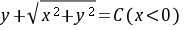 .
.
综合得,方程的通解为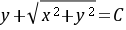 .
.
注:由于未给定自变量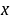 的取值范围,因此在此题求解过程中,引入新未知函数
的取值范围,因此在此题求解过程中,引入新未知函数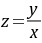 后得
后得
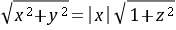 ,
,
从而,应当分别对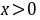 和
和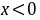 求解,在类似的问题中,这一点应当牢记.
求解,在类似的问题中,这一点应当牢记.
解析
考查要点:本题主要考查齐次微分方程的解法,通过变量替换将方程转化为可分离变量的形式,进而求解通解。
解题核心思路:
- 识别方程类型:观察方程右边的结构,发现分子和分母均为齐次函数(次数为1),因此属于齐次方程。
- 变量替换:令$y = z x$,将方程转化为关于$z$和$x$的可分离变量方程。
- 分离变量积分:对分离后的方程两边积分,得到关于$z$和$x$的关系式。
- 回代变量:将$z = \dfrac{y}{x}$代回,整理得到通解。
- 讨论$x$的符号:注意$x > 0$和$x < 0$时的解是否一致,最终合并结果。
破题关键点:
- 正确选择变量替换,将方程转化为可分离变量形式。
- 处理积分后的绝对值问题,确保解在$x > 0$和$x < 0$时的统一性。
变量替换与方程转化
令$y = z x$,则$\dfrac{dy}{dx} = z + x \dfrac{dz}{dx}$。
将$y = z x$代入原方程$\dfrac{dy}{dx} = \dfrac{y - \sqrt{x^2 + y^2}}{x}$,得:
$z + x \dfrac{dz}{dx} = \dfrac{z x - \sqrt{x^2 + (z x)^2}}{x} = z - \sqrt{1 + z^2}.$
消去两边的$z$,整理得:
$x \dfrac{dz}{dx} = -\sqrt{1 + z^2}.$
分离变量与积分
分离变量得:
$\dfrac{dz}{\sqrt{1 + z^2}} = -\dfrac{dx}{x}.$
两边积分:
$\int \dfrac{dz}{\sqrt{1 + z^2}} = -\int \dfrac{dx}{x}.$
左边积分结果为$\ln \left( z + \sqrt{1 + z^2} \right)$,右边积分结果为$-\ln |x| + C$,因此:
$\ln \left( z + \sqrt{1 + z^2} \right) = -\ln |x| + C.$
回代变量与整理
将$z = \dfrac{y}{x}$代入,得:
$\ln \left( \dfrac{y}{x} + \sqrt{1 + \left( \dfrac{y}{x} \right)^2} \right) = -\ln |x| + C.$
指数运算化简:
$\dfrac{y}{x} + \sqrt{\dfrac{x^2 + y^2}{x^2}} = \dfrac{C}{x}.$
两边乘以$x$,整理得通解:
$y + \sqrt{x^2 + y^2} = C.$
讨论$x$的符号
- 当$x > 0$时:直接代入上述结果,通解为$y + \sqrt{x^2 + y^2} = C$。
- 当$x < 0$时:令$t = -x > 0$,则方程形式不变,解仍为$y + \sqrt{x^2 + y^2} = C$。
综上,通解为:
$y + \sqrt{x^2 + y^2} = C \quad (x \neq 0).$