题目
[题目]函数 (x)=xsqrt (3-x) 在[0,3]上满足罗尔定-|||-理中的值是多少?

题目解答
答案
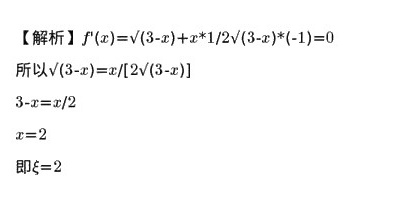
解析
罗尔定理的条件包括:函数在闭区间连续,开区间可导,且端点函数值相等。本题中,函数$f(x)=x\sqrt{3-x}$在区间$[0,3]$上满足这些条件。关键步骤是求导并解方程$f'(x)=0$,找到导数为零的点。
步骤1:验证罗尔定理的条件
- 连续性:$\sqrt{3-x}$在$[0,3]$上连续,乘以$x$后仍连续。
- 可导性:在开区间$(0,3)$内,函数可导。
- 端点值:$f(0)=0$,$f(3)=0$,满足$f(0)=f(3)$。
步骤2:求导数$f'(x)$
使用乘积法则:
$f'(x) = \frac{d}{dx}(x) \cdot \sqrt{3-x} + x \cdot \frac{d}{dx}(\sqrt{3-x}) = \sqrt{3-x} - \frac{x}{2\sqrt{3-x}}$
步骤3:解方程$f'(x)=0$
$\sqrt{3-x} - \frac{x}{2\sqrt{3-x}} = 0$
两边乘以$2\sqrt{3-x}$:
$2(3-x) - x = 0 \implies 6 - 3x = 0 \implies x = 2$