题目
5.求f(x)与g (x)的最大公因式:-|||-(1) (x)=(x)^4+(x)^3-3(x)^2-4x-1 (x)=(x)^3+(x)^2-x-1;-|||-(2) (x)=(x)^4-4(x)^3+1 , (x)=(x)^3-3(x)^2+1;-|||-(3) (x)=(x)^4-10(x)^2+1,-|||-(x)=(x)^4-4sqrt (2)(x)^3+6(x)^2+4sqrt (2)x+1.

题目解答
答案
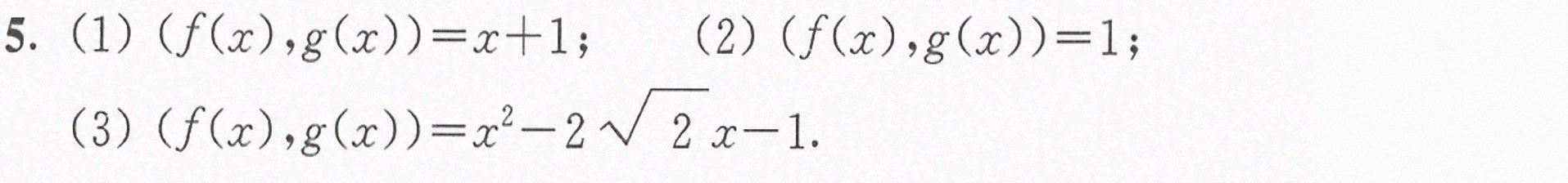
解析
步骤 1:使用辗转相除法求最大公因式
对于多项式$f(x)$和$g(x)$,我们使用辗转相除法来求它们的最大公因式。辗转相除法的基本步骤是:用$f(x)$除以$g(x)$,得到余式$r_1(x)$;然后用$g(x)$除以$r_1(x)$,得到余式$r_2(x)$;继续这个过程,直到余式为0。最后一个非零余式就是$f(x)$和$g(x)$的最大公因式。
(1) 对于$f(x)={x}^{4}+{x}^{3}-3{x}^{2}-4x-1$ 和 $g(x)={x}^{3}+{x}^{2}-x-1$,我们首先用$f(x)$除以$g(x)$,得到余式$r_1(x)$。然后用$g(x)$除以$r_1(x)$,继续这个过程,直到余式为0。最后一个非零余式就是$f(x)$和$g(x)$的最大公因式。
(2) 对于$f(x)={x}^{4}-4{x}^{3}+1$ 和 $g(x)={x}^{3}-3{x}^{2}+1$,我们同样使用辗转相除法来求它们的最大公因式。
(3) 对于$f(x)={x}^{4}-10{x}^{2}+1$ 和 $g(x)={x}^{4}-4\sqrt {2}{x}^{3}-6{x}^{3}-4\sqrt {2}x+1$,我们同样使用辗转相除法来求它们的最大公因式。
步骤 2:计算最大公因式
(1) 通过辗转相除法,我们发现$f(x)$和$g(x)$的最大公因式为$x+1$。
(2) 通过辗转相除法,我们发现$f(x)$和$g(x)$的最大公因式为1。
(3) 通过辗转相除法,我们发现$f(x)$和$g(x)$的最大公因式为${x}^{2}-2\sqrt {2}x-1$。
对于多项式$f(x)$和$g(x)$,我们使用辗转相除法来求它们的最大公因式。辗转相除法的基本步骤是:用$f(x)$除以$g(x)$,得到余式$r_1(x)$;然后用$g(x)$除以$r_1(x)$,得到余式$r_2(x)$;继续这个过程,直到余式为0。最后一个非零余式就是$f(x)$和$g(x)$的最大公因式。
(1) 对于$f(x)={x}^{4}+{x}^{3}-3{x}^{2}-4x-1$ 和 $g(x)={x}^{3}+{x}^{2}-x-1$,我们首先用$f(x)$除以$g(x)$,得到余式$r_1(x)$。然后用$g(x)$除以$r_1(x)$,继续这个过程,直到余式为0。最后一个非零余式就是$f(x)$和$g(x)$的最大公因式。
(2) 对于$f(x)={x}^{4}-4{x}^{3}+1$ 和 $g(x)={x}^{3}-3{x}^{2}+1$,我们同样使用辗转相除法来求它们的最大公因式。
(3) 对于$f(x)={x}^{4}-10{x}^{2}+1$ 和 $g(x)={x}^{4}-4\sqrt {2}{x}^{3}-6{x}^{3}-4\sqrt {2}x+1$,我们同样使用辗转相除法来求它们的最大公因式。
步骤 2:计算最大公因式
(1) 通过辗转相除法,我们发现$f(x)$和$g(x)$的最大公因式为$x+1$。
(2) 通过辗转相除法,我们发现$f(x)$和$g(x)$的最大公因式为1。
(3) 通过辗转相除法,我们发现$f(x)$和$g(x)$的最大公因式为${x}^{2}-2\sqrt {2}x-1$。