题目
设柱面的准线为 ) x=(y)^2+(z)^2 x=2z .,母线垂直于准线所在的平面,求这柱面的方程。.
设柱面的准线为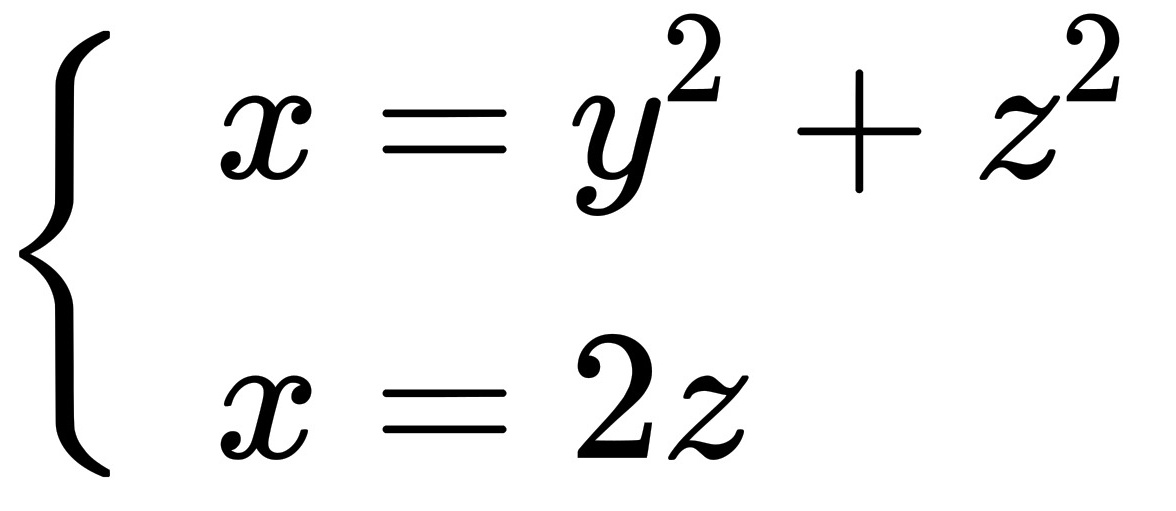 ,母线垂直于准线所在的平面,求这柱面的方程。
,母线垂直于准线所在的平面,求这柱面的方程。
题目解答
答案
由于,柱面的准线为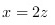 ,
,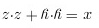
而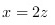 为一平面.故它就是准线所在平面.即所求柱面的母线垂直于此平面.
为一平面.故它就是准线所在平面.即所求柱面的母线垂直于此平面.
此平面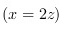 的法向量为n=(1,0 ,-2),此即为所求柱面的准线的方向向量.
的法向量为n=(1,0 ,-2),此即为所求柱面的准线的方向向量.
设: 为准线上的任意一点,则过该点的母线方程为:
为准线上的任意一点,则过该点的母线方程为: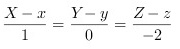 其中P(X,Y,Z)为母线上点坐标.而
其中P(X,Y,Z)为母线上点坐标.而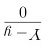 系指
系指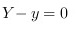
上式即: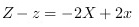 ,
,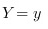
以下是要由上式和原准线方程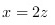 ,
,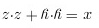 从中消去x,y,z 而得出关于(X,Y,Z)的方程,即所求柱面的方程.
从中消去x,y,z 而得出关于(X,Y,Z)的方程,即所求柱面的方程.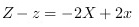 ,(1)
,(1)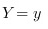 ,(2)
,(2)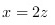 ,(3)
,(3)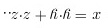 即
即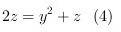
由(3),(1)变为: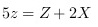 ,(5)
,(5)
由(3) ,(4)变为: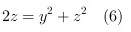
将:(2),(5)代入(6)得: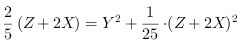
整理得: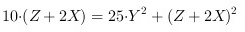
解析
考查要点:本题主要考查柱面方程的求解方法,涉及准线、母线方向向量的确定,以及参数方程的消元技巧。
解题核心思路:
- 确定准线所在的平面:准线由两个平面方程的交线构成,其中关键平面为$x=2z$。
- 求母线方向向量:母线垂直于准线所在平面$x=2z$,其法向量为$(1,0,-2)$,即为母线方向向量。
- 建立母线方程:以准线上任意点$(x,y,z)$为起点,沿母线方向延伸,得到参数方程。
- 消去参数:通过准线方程和母线方程,消去中间变量,得到关于$(X,Y,Z)$的方程。
破题关键点:
- 准线参数化:将准线表示为参数方程,便于后续推导。
- 母线方向向量的确定:直接利用平面法向量作为母线方向。
- 消元法:通过代数运算消去参数,得到最终方程。
步骤1:确定准线参数方程
准线由$x=y^2$和$x=2z$的交线构成,参数化为:
$\begin{cases}x = t^2 \\y = t \\z = \dfrac{t^2}{2}\end{cases}$
步骤2:求母线方向向量
准线所在平面$x=2z$的法向量为$\mathbf{n}=(1,0,-2)$,故母线方向向量为$(1,0,-2)$。
步骤3:建立母线方程
准线上任一点$(t^2, t, \dfrac{t^2}{2})$,母线方程为:
$\begin{cases}X = t^2 + \lambda \\Y = t \\Z = \dfrac{t^2}{2} - 2\lambda\end{cases}$
步骤4:消去参数
- 由$Y = t$得$t = Y$,代入$X$和$Z$:
$X = Y^2 + \lambda \quad \Rightarrow \quad \lambda = X - Y^2$ - 代入$Z$的表达式:
$Z = \dfrac{Y^2}{2} - 2(X - Y^2) = \dfrac{5Y^2}{2} - 2X$ - 整理得柱面方程:
$4X + 2Z = 5Y^2$