题目
定积分(int )_(0)^3(2)^xdx=( ).A.(int )_(0)^3(2)^xdx=B.(int )_(0)^3(2)^xdx=C.(int )_(0)^3(2)^xdx=D.(int )_(0)^3(2)^xdx=
定积分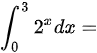 ( ).
( ).
A.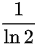
B.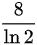
C.
D.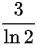
题目解答
答案
本题考查定积分的计算.
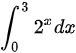
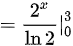
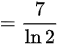
故本题答案选C,排除A,B,D.
解析
考查要点:本题主要考查定积分的计算,特别是对指数函数$a^x$的积分公式的应用。
解题核心思路:
- 积分公式:$\int a^x dx = \dfrac{a^x}{\ln a} + C$(其中$a > 0$且$a \neq 1$)。
- 定积分计算:代入上下限后,用上限值减去下限值。
破题关键点:
- 正确应用指数函数的积分公式,注意分母为$\ln 2$。
- 计算上下限代入后的差值时,避免符号错误。
步骤1:应用积分公式
根据指数函数的积分公式:
$\int 2^x dx = \dfrac{2^x}{\ln 2} + C$
步骤2:代入上下限
计算定积分$\int_{0}^{3} 2^x dx$:
$\left. \dfrac{2^x}{\ln 2} \right|_{0}^{3} = \dfrac{2^3}{\ln 2} - \dfrac{2^0}{\ln 2}$
步骤3:化简结果
计算具体数值:
$\dfrac{8}{\ln 2} - \dfrac{1}{\ln 2} = \dfrac{7}{\ln 2}$
结论:最终结果为$\dfrac{7}{\ln 2}$,对应选项C。