题目
通过点_(1)(1,-5,1) _(2)(2,1,-2)且与_(1)(1,-5,1) _(2)(2,1,-2)轴平行的平面方程为A._(1)(1,-5,1) _(2)(2,1,-2)B._(1)(1,-5,1) _(2)(2,1,-2)C._(1)(1,-5,1) _(2)(2,1,-2)D._(1)(1,-5,1) _(2)(2,1,-2)
通过点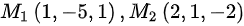
且与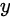
轴平行的平面方程为
A.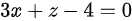
B.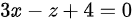
C.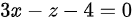
D.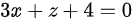
题目解答
答案
由于直线过点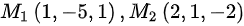，则在平面内有一个向量为：
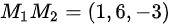，同时又因为直线与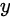轴平行，则该平面内的另一向量为
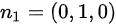，将这两个向量叉乘可以得到平面的法向量为：
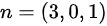，又因为平面过点
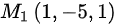，由此可以得到平面的方程为：。
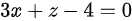解析
步骤 1：确定平面内的向量
由于直线过点${M}_{1}(1,-5,1)$和${M}_{2}(2,1,-2)$，则在平面内有一个向量为：${M}_{1}{M}_{2}=(2-1,1-(-5),-2-1)=(1,6,-3)$。
步骤 2：确定平面内的另一个向量
同时又因为直线与ce轴平行，即与y轴平行，因此该平面内的另一向量为${n}_{1}=(0,1,0)$。
步骤 3：计算平面的法向量
将这两个向量叉乘可以得到平面的法向量为：$n={M}_{1}{M}_{2} \times {n}_{1}=(1,6,-3) \times (0,1,0)=(6 \times 0 - (-3) \times 1, -3 \times 0 - 1 \times 0, 1 \times 1 - 6 \times 0)=(3,0,1)$。
步骤 4：确定平面方程
又因为平面过点${M}_{1}(1,-5,1)$，由此可以得到平面的方程为：$3(x-1)+0(y+5)+1(z-1)=0$，即$3x+z-4=0$。
由于直线过点${M}_{1}(1,-5,1)$和${M}_{2}(2,1,-2)$，则在平面内有一个向量为：${M}_{1}{M}_{2}=(2-1,1-(-5),-2-1)=(1,6,-3)$。
步骤 2：确定平面内的另一个向量
同时又因为直线与ce轴平行，即与y轴平行，因此该平面内的另一向量为${n}_{1}=(0,1,0)$。
步骤 3：计算平面的法向量
将这两个向量叉乘可以得到平面的法向量为：$n={M}_{1}{M}_{2} \times {n}_{1}=(1,6,-3) \times (0,1,0)=(6 \times 0 - (-3) \times 1, -3 \times 0 - 1 \times 0, 1 \times 1 - 6 \times 0)=(3,0,1)$。
步骤 4：确定平面方程
又因为平面过点${M}_{1}(1,-5,1)$，由此可以得到平面的方程为：$3(x-1)+0(y+5)+1(z-1)=0$，即$3x+z-4=0$。