题目
求微分方程'+ycos x=2(e)^-sin x满足初始条件'+ycos x=2(e)^-sin x的特解。
求微分方程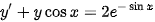 满足初始条件
满足初始条件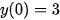 的特解。
的特解。
题目解答
答案
微分方程为非齐次线性方程,令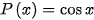 ,
,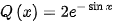 ,则方程的通解为
,则方程的通解为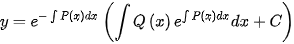
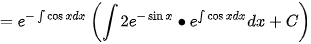
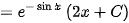
然后将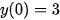 代入即可求出特解。
代入即可求出特解。
令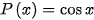 ,
,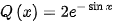 ,则方程的通解为
,则方程的通解为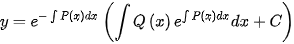
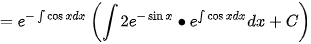
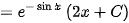
将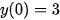 代入得
代入得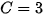
∴ 特解为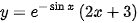
故答案为: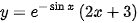
解析
步骤 1:确定方程类型
给定的微分方程$y'+y\cos x=2{e}^{-\sin x}$是一个一阶线性非齐次微分方程,其中$P(x)=\cos x$,$Q(x)=2{e}^{-\sin x}$。
步骤 2:求解齐次方程
首先求解对应的齐次方程$y'+y\cos x=0$。该方程的通解为$y={e}^{-\int P(x)dx}={e}^{-\int \cos xdx}={e}^{-\sin x}$。
步骤 3:求解非齐次方程
对于非齐次方程$y'+y\cos x=2{e}^{-\sin x}$,其通解形式为$y={e}^{-\int P(x)dx}(\int Q(x){e}^{\int P(x)dx}dx+C)$。将$P(x)$和$Q(x)$代入,得到$y={e}^{-\sin x}(\int 2{e}^{-\sin x}{e}^{\sin x}dx+C)$。简化后得到$y={e}^{-\sin x}(2x+C)$。
步骤 4:应用初始条件
将初始条件$y(0)=3$代入通解$y={e}^{-\sin x}(2x+C)$,得到$3={e}^{-\sin 0}(2\cdot0+C)$,即$3=C$。因此,特解为$y={e}^{-\sin x}(2x+3)$。
给定的微分方程$y'+y\cos x=2{e}^{-\sin x}$是一个一阶线性非齐次微分方程,其中$P(x)=\cos x$,$Q(x)=2{e}^{-\sin x}$。
步骤 2:求解齐次方程
首先求解对应的齐次方程$y'+y\cos x=0$。该方程的通解为$y={e}^{-\int P(x)dx}={e}^{-\int \cos xdx}={e}^{-\sin x}$。
步骤 3:求解非齐次方程
对于非齐次方程$y'+y\cos x=2{e}^{-\sin x}$,其通解形式为$y={e}^{-\int P(x)dx}(\int Q(x){e}^{\int P(x)dx}dx+C)$。将$P(x)$和$Q(x)$代入,得到$y={e}^{-\sin x}(\int 2{e}^{-\sin x}{e}^{\sin x}dx+C)$。简化后得到$y={e}^{-\sin x}(2x+C)$。
步骤 4:应用初始条件
将初始条件$y(0)=3$代入通解$y={e}^{-\sin x}(2x+C)$,得到$3={e}^{-\sin 0}(2\cdot0+C)$,即$3=C$。因此,特解为$y={e}^{-\sin x}(2x+3)$。