题目
求由曲线 y=x+2 和 =(x)^2 所围成的平面图形的面积。
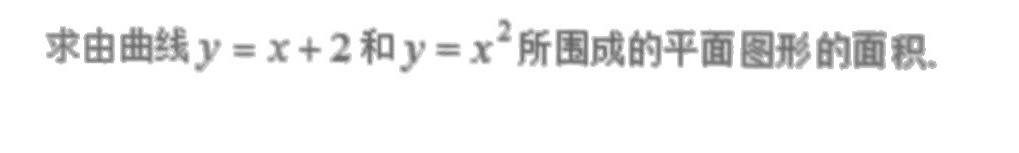
题目解答
答案

解析
步骤 1:确定交点
首先,我们需要找到曲线 $y=x+2$ 和 $y=x^2$ 的交点。为此,我们解方程 $x+2=x^2$。
步骤 2:解方程
解方程 $x^2-x-2=0$,得到 $x=-1$ 和 $x=2$。
步骤 3:计算面积
根据交点,我们计算由曲线 $y=x+2$ 和 $y=x^2$ 所围成的平面图形的面积。面积可以通过计算两个函数在 $x=-1$ 到 $x=2$ 之间的积分差来得到。
步骤 4:积分计算
计算 $\int_{-1}^{2} (x+2-x^2) dx$。
步骤 5:求解
计算积分 $\int_{-1}^{2} (x+2-x^2) dx = \left[\frac{1}{2}x^2+2x-\frac{1}{3}x^3\right]_{-1}^{2}$。
步骤 6:代入上下限
代入上下限,得到 $\left(\frac{1}{2}(2)^2+2(2)-\frac{1}{3}(2)^3\right) - \left(\frac{1}{2}(-1)^2+2(-1)-\frac{1}{3}(-1)^3\right)$。
步骤 7:计算结果
计算得到 $\left(2+4-\frac{8}{3}\right) - \left(\frac{1}{2}-2+\frac{1}{3}\right) = \frac{9}{2}$。
首先,我们需要找到曲线 $y=x+2$ 和 $y=x^2$ 的交点。为此,我们解方程 $x+2=x^2$。
步骤 2:解方程
解方程 $x^2-x-2=0$,得到 $x=-1$ 和 $x=2$。
步骤 3:计算面积
根据交点,我们计算由曲线 $y=x+2$ 和 $y=x^2$ 所围成的平面图形的面积。面积可以通过计算两个函数在 $x=-1$ 到 $x=2$ 之间的积分差来得到。
步骤 4:积分计算
计算 $\int_{-1}^{2} (x+2-x^2) dx$。
步骤 5:求解
计算积分 $\int_{-1}^{2} (x+2-x^2) dx = \left[\frac{1}{2}x^2+2x-\frac{1}{3}x^3\right]_{-1}^{2}$。
步骤 6:代入上下限
代入上下限,得到 $\left(\frac{1}{2}(2)^2+2(2)-\frac{1}{3}(2)^3\right) - \left(\frac{1}{2}(-1)^2+2(-1)-\frac{1}{3}(-1)^3\right)$。
步骤 7:计算结果
计算得到 $\left(2+4-\frac{8}{3}\right) - \left(\frac{1}{2}-2+\frac{1}{3}\right) = \frac{9}{2}$。